Question

【题目】设函数(a>0，且a≠1)的反函数为，函数y=g(x)的图像与的图像关于点(a,0)对称。

（1）求函数y=g(x)的解析式。

（2）是否存在实数a，使得当时，恒有成立？若存在，求出a的取值范围；若不存在，说明理由。

Answer 1

【答案】（1）；（2）见解析

【解析】

（1）由，得.

又y=g(x)的图像与的图像关于点( a,0)对称，则有

.

（2）假设存在实数a，使得当时，不等式恒成立，则有，即.

由3a<a+2及a>0，得0<a<1.

因此，，即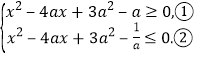

解式①得.

由题设知.

所以，.

结合0<a<1，解得.

对于式②，令.

则[a+2，a+3]是不等式h(x)≤0的解集的子集的充要条件是

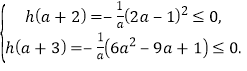
结合0<a<1，解得.

综上所述存在，使得x∈[ a+2，a+3]时，不等式恒成立.