题目内容
【题目】己知向量![]() ,
,![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值和最小值及相应的
的最大值和最小值及相应的![]() 的值;
的值;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数![]() 的图象,若
的图象,若![]() 在
在![]() 有两个不同的解,求实数
有两个不同的解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)最大值为2,此时![]() ;最小值为-1,此时
;最小值为-1,此时![]() . (2)
. (2)![]()
【解析】
(1)根据向量数量积坐标公式,列出函数![]() ,再根据函数图像过定点,求解函数解析式,当
,再根据函数图像过定点,求解函数解析式,当![]() 时,解出
时,解出![]() 的范围,根据三角函数性质,可求最值;
的范围,根据三角函数性质,可求最值;
(2)根据三角函数平移伸缩变换,写出![]() 解析式,画出
解析式,画出![]() 在
在![]() 上的图象,根据图像即可求解参数取值范围.
上的图象,根据图像即可求解参数取值范围.
解:(1)由题意知![]() .
.
根据![]() 的图象过点
的图象过点![]() 和
和![]() ,得到
,得到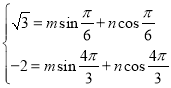 ,
,
解得![]() ,
,![]() .
.
![]()
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 最大值为2,此时
最大值为2,此时![]() ,
,
![]() 最小值为-1,此时
最小值为-1,此时![]() .
.
(2)将函数![]() 的图象向右平移一个单位
的图象向右平移一个单位
得![]() ,
,
再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得![]()
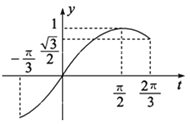
令![]() ,
,![]() ,如图当
,如图当![]() 时,
时,
![]() 在
在![]() 有两个不同的解
有两个不同的解
∴![]() ,即
,即![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
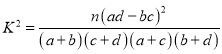 (其中
(其中 ![]() )
)



