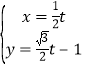Question

【题目】对每一个实数a，将抛物线记为。

（1）求所有的交集；

（2）求所有的焦点的轨迹方程;

（3）求所有的直线l，使其与所有的都有公共点;

（4）求所有的a，使得存在一条以y轴为对称轴且过点的开口向下的抛物线与相切。

Answer 1

【答案】（1）；（2）；（3）见解析；（4）

【解析】

（1）设

则

即.

此方程只有一个解，

从而.

所以交集为点.

（2）的顶点坐标为，而焦点在顶点的正上方,且距离为，焦点坐标为

消去a得.

故所有的的焦点的轨迹方程是.

（3）首先，直线 (t为任意实数)符合要求.

下面考虑与x轴不垂直的直线 (k、b为待定的常数)，则得方程，即.

令其判别式得 ①

因为式①对每一个实数a都成立，则其判别式.解得.

综上，所求的直线为（t为任意实数）和,其中.

(4)易知，过点、以y轴为对称轴、开口向下的抛物线方程为.

由于此抛物线与相切，所以，.

即有唯一的实数解x.

从而，，即.

所以，.

由于，，故，即.