题目内容
10.先解答(1),再通过结构类比解答(2):(1)求证:tan(x+$\frac{π}{4}$)=$\frac{1+tanx}{1-tanx}$;
(2)设x∈R,试问f(x+1)=$\frac{1+f(x)}{1-f(x)}$是周期函数吗?证明你的结论.
分析 (1)根据两角和的正切公式,把所给的等式的右边展开,利用特殊角的三角函数最后得到和右边的式子相等,等式得证.
(2)猜想是周期函数,利用周期函数的定义证明即可.
解答 解:(1)证明:tan(x+$\frac{π}{4}$)=$\frac{tanx+tan\frac{π}{4}}{1-tanxtan\frac{π}{4}}$=$\frac{1+tanx}{1-tanx}$;
(2)猜想f(x)是以4为周期的周期函数.
证明:因为f(x+2×$\frac{1}{2}$)=f[(x+$\frac{1}{2}$)+$\frac{1}{2}$]=$\frac{1+f(x+\frac{1}{2})}{1-f(x+\frac{1}{2})}$=$\frac{1+\frac{1+f(x)}{1-f(x)}}{1-\frac{1+f(x)}{1-f(x)}}$=-$\frac{1}{f(x)}$,
所以f(x+4)=f[(x+2)+2]=-$\frac{1}{f(x+2)}$=f(x),
所以f(x)是以4为周期的周期函数.
点评 本题考查三角函数的化简求值,周期的应用,基本知识的考查.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
20.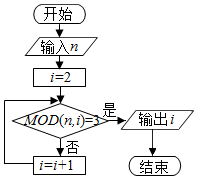 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(7,3)=1,如图是一个算法的程序框图,当输入的n值为15时,输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(7,3)=1,如图是一个算法的程序框图,当输入的n值为15时,输出的结果为( )
 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(7,3)=1,如图是一个算法的程序框图,当输入的n值为15时,输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(7,3)=1,如图是一个算法的程序框图,当输入的n值为15时,输出的结果为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
15.在等差数列{an}中,a1=81,公差d=-7,则前( )项和最大.
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
19.已知集合M={m2,5},N={1,4},则“m=2”是“M∩N={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
15.已知集合P={x|x2=4},集合Q={x|ax=4},若Q⊆P,则a的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 0,2,或-2 |