题目内容
给出下列说法:
①命题“若x=kπ(k∈Z),则sin2x=0”的否命题是真命题;
②命题“?x∈R,2 x2+x+1<
”是假命题且其否定为“?x∈R,2 x2+x+1≥
”;
③已知a,b∈R,则“a>b”是“2a>2b+1“的必要不充分条件.
其中说法正确的是( )
①命题“若x=kπ(k∈Z),则sin2x=0”的否命题是真命题;
②命题“?x∈R,2 x2+x+1<
| 2 |
| 2 |
③已知a,b∈R,则“a>b”是“2a>2b+1“的必要不充分条件.
其中说法正确的是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:求出使sin2x=0的x值判断①;由基本不等式得到2 x2+x+1>
并写出原命题的否定判断②;举例说明③正确.
| 2 |
解答:
解:若sin2x=0,则2x=kπ,即x=
,k∈Z,故①错误;
2 x2+x+1=2(x+
)2+
≥2
>
,命题“?x∈R,2 x2+x+1<
”是假命题,其否定为“?x∈R,2 x2+x+1≥
”,故②正确;
当a=0,b=-1时,由a>b不能得到2a>2b+1,反之成立.故③正确.
∴正确的命题是②③.
故选:C.
| kπ |
| 2 |
2 x2+x+1=2(x+
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 2 |
| 2 |
当a=0,b=-1时,由a>b不能得到2a>2b+1,反之成立.故③正确.
∴正确的命题是②③.
故选:C.
点评:本题考查了命题的真假判断与应用,考查了充分条件和必要条件的判定方法,考查了命题的否定,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知幂函数f(x)=(m-3)xm,则下列关于f(x)的说法不正确的是( )
| A、f(x)的图象过原点 |
| B、f(x)的图象关于原点对称 |
| C、f(x)的图象关于y轴对称 |
| D、f(x)=x4 |
集合A={x|2<x<7},B={x|3≤x<10},A∩B=( )
| A、(2,10) |
| B、[3,7) |
| C、(2,3] |
| D、(7,10) |
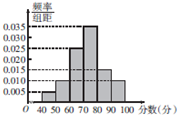 某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )
某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )| A、120 | B、150 |
| C、180 | D、200 |
设a2-a>0,函数y=a|x|(a>0,a≠1)的图象形状大致是( )
A、 |
B、 |
C、 |
D、 |
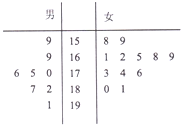 第117届中国进出口商品交易会(简称2015年春季交广会)将于2015年4月15日在广州市举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如下茎叶图(单位:m),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.
第117届中国进出口商品交易会(简称2015年春季交广会)将于2015年4月15日在广州市举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如下茎叶图(单位:m),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.