题目内容
已知圆的方程为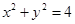 ,过点
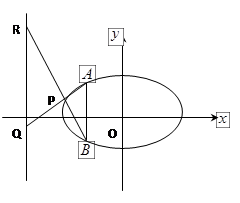
,过点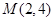 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为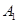 、
、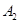 ,直线
,直线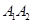 恰好经过椭圆
恰好经过椭圆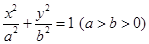 的右顶点和上顶点.
的右顶点和上顶点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设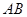 是椭圆
是椭圆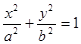 (
(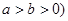 垂直于
垂直于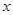 轴的一条弦,
轴的一条弦,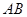 所在直线的方程为
所在直线的方程为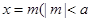 且
且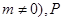 是椭圆上异于
是椭圆上异于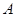 、
、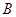 的任意一点,直线
的任意一点,直线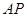 、
、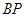 分别交定直线
分别交定直线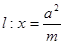 于两点
于两点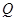 、
、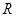 ,求证
,求证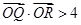 .
.
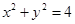 ,过点
,过点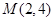 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为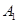 、
、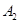 ,直线
,直线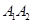 恰好经过椭圆
恰好经过椭圆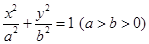 的右顶点和上顶点.
的右顶点和上顶点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设
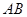 是椭圆
是椭圆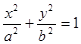 (
(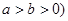 垂直于
垂直于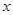 轴的一条弦,
轴的一条弦,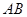 所在直线的方程为
所在直线的方程为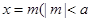 且
且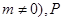 是椭圆上异于
是椭圆上异于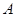 、
、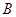 的任意一点,直线
的任意一点,直线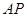 、
、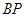 分别交定直线
分别交定直线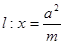 于两点
于两点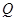 、
、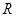 ,求证
,求证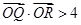 .
. (Ⅰ) (Ⅱ)联立方程组表示出向量
(Ⅱ)联立方程组表示出向量 ,再证.
,再证.
 (Ⅱ)联立方程组表示出向量
(Ⅱ)联立方程组表示出向量 ,再证.
,再证.试题分析:(Ⅰ) 观察知,
 是圆的一条切线,切点为
是圆的一条切线,切点为 ,
, 设
 为圆心,根据圆的切线性质,
为圆心,根据圆的切线性质, ,
, 所以
 , 所以直线
, 所以直线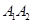 的方程为
的方程为 .
.线
 与
与 轴相交于
轴相交于 ,依题意
,依题意 ,所求椭圆的方程为
,所求椭圆的方程为
(Ⅱ) 椭圆方程为
 ,设
,设


则有
 ,
,
在直线
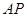 的方程
的方程 中,令
中,令 ,整理得
,整理得 ①
①同理,
 ②
② ①
 ②,并将
②,并将
 代入得
代入得

=
 =
= =
= .
.而
 =
=
∵
 且
且 ,∴
,∴
∴
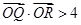
点评:本题考查直线与圆锥曲线的位置关系,考查椭圆的标准方程,考查数形结合思想,考查学生的运算能力、分析问题解决问题的能力,难度较大.

练习册系列答案
相关题目
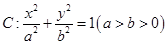 的左右焦点分别为
的左右焦点分别为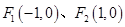 ,且经过点
,且经过点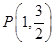 ,
,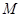 为椭圆上的动点,以
为椭圆上的动点,以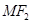 为半径作圆
为半径作圆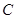 的方程;
的方程;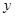 轴有两个交点,求点
轴有两个交点,求点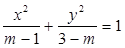 表示椭圆,则
表示椭圆,则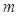 的取值范围是______________.
的取值范围是______________.  中,椭圆
中,椭圆 的标准方程为
的标准方程为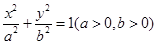 ,右焦点为
,右焦点为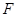 ,右准线为
,右准线为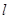 ,短轴的一个端点
,短轴的一个端点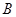 . 设原点到直线
. 设原点到直线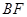 的距离为
的距离为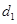 ,
,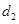 . 若
. 若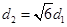 ,则椭圆
,则椭圆 中,
中,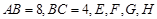 分别为四边的中点,且都在坐标轴上,设
分别为四边的中点,且都在坐标轴上,设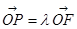 ,
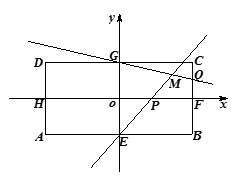
,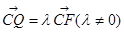 .
.
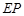 与
与 的交点
的交点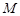 的轨迹
的轨迹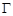 的方程;
的方程;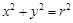
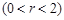 上一点
上一点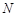 作圆的切线与轨迹
作圆的切线与轨迹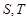 两点,若
两点,若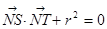 ,试求出
,试求出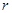 的值.
的值.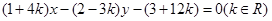 所经过的定点
所经过的定点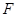 恰好是椭圆
恰好是椭圆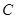 的一个焦点,且椭圆
的一个焦点,且椭圆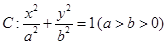 .
.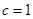 ,且
,且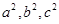 成等差数列,求椭圆
成等差数列,求椭圆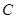 的方程;
的方程;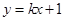 相交于
相交于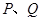 两点,求
两点,求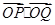 的取值范围.
的取值范围.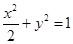 的左焦点
的左焦点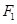 作直线
作直线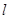 交椭圆于
交椭圆于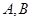 两点,
两点,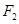 是椭圆右焦点,则
是椭圆右焦点,则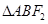 的周长为( )
的周长为( )
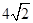


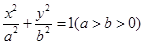 的上顶点坐标为
的上顶点坐标为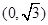 ,离心率为
,离心率为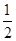 .
.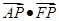 的取值范围.
的取值范围.