题目内容
12.设全集U=R,集合A={x|(x+1)(x-3)<0},B={x|x-1≥0},则图中阴影部分所表示的集合为( )
| A. | {x|x≤-1或x≥3} | B. | {x|x<1或x≥3} | C. | {x|x≤1} | D. | {x|x≤-1} |
分析 由阴影部分表示的集合为∁U(A∪B),然后根据集合的运算即可.
解答 解:由图象可知阴影部分对应的集合为∁U(A∪B),
A={x|(x+1)(x-3)<0}=(-1,3),
∵B={x|x-1≥0},
∴A∪B=(-1,+∞),
则∁U(A∪B)=(-∞,-1],
故选D.
点评 本题主要考查集合的基本运算,利用Venn图确定集合的关系是解决本题的关键.

练习册系列答案
相关题目
20.等差数列{an}的公差d≠0,且a3,a5,a15成等比数列,若a5=5,Sn为数列{an}的前n项和,则数列{$\frac{{S}_{n}}{n}$}的前n项和取最小值时的n为( )
| A. | 3 | B. | 3或4 | C. | 4或5 | D. | 5 |
4.已知△ABC中,内角A,B,C的对边分别为a,b,c,b=2,B=45°,若三角形有两解,则a的取值范围是( )
| A. | a>2 | B. | 0<a<2 | C. | 2<a<2$\sqrt{2}$ | D. | 2<a<2$\sqrt{3}$ |
1.若x,y满足$\left\{\begin{array}{l}{y-1≥0}\\{x-y+1≥0}\\{x-1≤0}\end{array}\right.$,则x+y的最小值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
2.若sinθ>cosθ,且tanθ<0,则角θ的终边位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
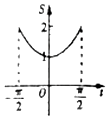
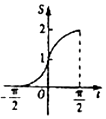
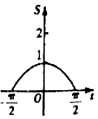
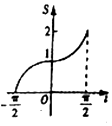
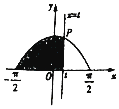 在函数y=cosx,$x∈[{-\frac{π}{2},\frac{π}{2}}]$的图象上有一点P(t,cost),若该函数的图象与x轴、直线$x=-\frac{π}{2},x=t$,围成图形(如图阴影部分)的面积为S,则函数S=g(t)的图象大致是( )
在函数y=cosx,$x∈[{-\frac{π}{2},\frac{π}{2}}]$的图象上有一点P(t,cost),若该函数的图象与x轴、直线$x=-\frac{π}{2},x=t$,围成图形(如图阴影部分)的面积为S,则函数S=g(t)的图象大致是( )