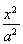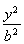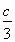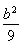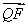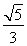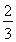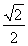题目内容
已知P是椭圆C:
(1)若椭圆的焦距为6,求椭圆C的方程;
(2)若![]() ·
·![]() =0,且
=0,且![]() =λ
=λ![]() ,求实数λ的值.
,求实数λ的值.
(1)解法一:由![]() =3
=3![]() ,得a+3=3(
,得a+3=3(![]() -3),a=4.
-3),a=4.
∴b2=a2-c2=7,
从而椭圆方程是![]() =1.
=1.
解法二:记c=![]() ,由
,由![]() =3
=3![]() ,得a+c=3(
,得a+c=3(![]() -c)=
-c)=![]() ,
,
∵a+c>0,∴3a=4c.
又2c=6,c=3,∴b2=a2-c2=7,
从而椭圆方程是![]() =1.
=1.
(2)解法一:点P(xP,yP)同时满足![]() =1和(x+a)(x-c)+y2=0.
=1和(x+a)(x-c)+y2=0.
消去y2并整理得c2x2+a2(a-c)x-a3c+a2b2=0,
此方程必有两实根,一根是点A的横坐标-a,另一根是点P的横坐标xP,
-a·xP=![]() ,xP=
,xP=![]() .
.
∴xP-xA=![]() -(-a)=
-(-a)=![]() ,xm-xP=
,xm-xP=![]() -
-![]() =
=![]() .
.
∴![]() =|
=|![]() |=|
|=|![]() |=|
|=|![]() |,
|,
由![]() =
=![]() 代入上式可得
代入上式可得![]() =2.
=2.
∴![]() =
=![]() ,λ=2.
,λ=2.
解法二:由(1) ![]() =3
=3![]() ,3a=4c,
,3a=4c,
可设a=4t,c=3t,则b=![]() t,
t,
椭圆方程可为![]() =1,
=1,
即7x2+16y2=112t2.
设直线AM的方程为y=k(x+4t)(k存在且k≠0),
代入7x2+16y2=112t2,
整理得(16k2+7)x2+128k2tx+256k2t2-112t2=0,
此方程两根为A、P两点的横坐标,
由韦达定理有-4t·xP=![]() ,xP=
,xP=![]() ,
,
∴xP=![]() ,
,
从而yP=![]() .
.
由于kPF=![]() ,k2=
,k2=![]() ,
,
![]() =|
=|![]() |=
|= =
=![]() .
.
∴![]() =2
=2![]() ,λ=2.
,λ=2.

 阅读快车系列答案
阅读快车系列答案 已知P是椭圆
已知P是椭圆