题目内容
3.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的短轴长为4,焦距为2.(1)求C的方程;
(2)过椭圆C的左焦点F1作倾斜角为45°的直线l,直线l与椭圆相交于A、B两点,求AB的长.
分析 (1)椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的短轴长为4,焦距为2.可得a,b;
(2)过F1倾斜角为45°的直线l:y=x+1.
把y=x+1.代入圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.得7x2+8x-8=0,
由韦达定理及弦长公式可计算AB.
解答 解:(1)∵椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的短轴长为4,焦距为2.∴b=2,c=1,a=$\sqrt{5}$,
椭圆的方程为:$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$.
(2)由(1)得椭圆C的左焦点F1(-1,0),过F1倾斜角为45°的直线l:y=x+1.
把y=x+1.代入圆的方程为:$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$.得9x2+10x-15=0,
设A(x1,y1)、B(x2,y2),x1+x2=-$\frac{10}{9}$,x1x2=-$\frac{15}{9}$,
AB=$\sqrt{1+{1}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}=\frac{8\sqrt{10}}{9}$
点评 本题考查了直线与椭圆的位置关系,及弦长公式,属于基础题.

练习册系列答案
相关题目
15.在平面直角坐标系xOy中,已知△ABC的顶点A(0,4),C(0,-4),顶点B在椭圆$\frac{x^2}{9}+\frac{y^2}{25}=1$上,则$\frac{sin(A+C)}{sinA+sinC}$=( )
| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
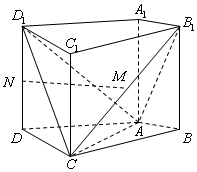 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.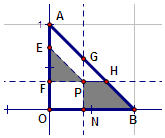 △AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.
△AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.