题目内容
已知函数f（x）=2sinxcosx+
（cos2x-sin2x）
（1）求f（x）的最小正周期和对称中心；
（2）求f（x）在区间[-
，
]上的取值范围．
| 3 |
（1）求f（x）的最小正周期和对称中心；
（2）求f（x）在区间[-
| π |
| 3 |
| π |
| 2 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：计算题,三角函数的求值,三角函数的图像与性质
分析：（1）将函数进行化简，根据三角函数的图象和性质即可求函数f（x）的最小正周期和对称中心坐标；
（2）根据x的范围求出这个角的范围，利用正弦函数的图象与性质即可求出f（x）的取值范围．
（2）根据x的范围求出这个角的范围，利用正弦函数的图象与性质即可求出f（x）的取值范围．
解答：
解：（1）∵f（x）=2sinxcosx+
（cos2x-sin2x）=sin2x+
cos2x=2sin（2x+
）．
∴T=
=π，
∴对称中心横坐标x应该满足2x+
=kπ，即x=
-
，k∈Z，此时y=0，
所以对称中心为（
-
，0）．
（2）∵-
≤x≤
，∴-
≤2x+
≤
，
∴-
≤sin（2x+
）≤1，即-
≤2sin（2x+
）≤2，
则f（x）取值范围为（-
，2]．
| 3 |
| 3 |
| π |
| 3 |
∴T=
| 2π |
| 2 |
∴对称中心横坐标x应该满足2x+
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
所以对称中心为（
| kπ |
| 2 |
| π |
| 6 |
（2）∵-
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
| 3 |
| π |
| 3 |
则f（x）取值范围为（-
| 3 |
点评：本题主要考查三角函数的图象和性质，三角函数的周期性及其求法，利用三角函数的关系式进行化简是解决本题的关键，属于基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知α∈（
，π），且sinα•cosα=-
，则sinα-cosα的值是（ ）
| 3π |
| 4 |
| ||
| 4 |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
设α为平面，m，n为直线（ ）
| A、若m，n与α所成角相等，则m∥n |
| B、若m∥α，n∥α，则m∥n |
| C、若m，n与α所成角互余，则m⊥n |
| D、若m∥α，n⊥α，则m⊥n |
设变量x，y满足约束条件：
，则z=x-3y+4的最大值为（ ）
|
| A、8 | B、6 | C、4 | D、2 |
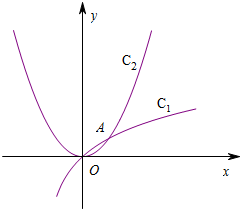函数f（x）=x2和g（x）=log3（x+1）的部分图象如图所示，设两函数的图象交于点O（0，0），A（x0，y0）．