题目内容
15．已知数列{bn}为等比数列，且b1008=e（e为自然对数的底数），数列{an}首项为1，且an+1=an•bn，则lna2016的值为2015．分析 由an+1=an•bn，推导出a2016=b1×b2×b3×b4×…×b2015=${{b}_{1008}}^{2015}$=e2015，由此能求出lna2016．
解答 解：∵数列{bn}为等比数列，且b1008=e（e为自然对数的底数），数列{an}首项为1，且an+1=an•bn，
∴a2016=b1×b2×b3×b4×…×b2015=${{b}_{1008}}^{2015}$=e2015，
lna2016=lne2015=2015．
故答案为：2015．
点评 本题考查对数值的求法，是基础题，解题时要认真审题，注意等比数列性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
5．某几何体的三视图如图所示，则该几何体的表面积为（ ）
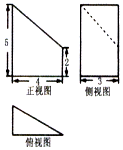
| A． | 45 | B． | $45+\frac{{9\sqrt{2}}}{2}$ | C． | $\frac{117}{2}$ | D． | 60 |
如图所示的流程图，当输入n的值为10时，则输出的S的值为30．
3．已知ω＞0，将函数f（x）=cosωx的图象向右平移$\frac{π}{2}$个单位后得到函数$g（x）=sin（{ωx-\frac{π}{4}}）$的图象，则ω的最小值是（ ）
| A． | $\frac{3}{2}$ | B． | 3 | C． | $\frac{4}{3}$ | D． | $\frac{2}{3}$ |
10．
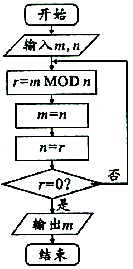如图所示，程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“mMODn”表示m除以n的余数），若输入的m，n分别为2016，612，则输出的m=（ ）
如图所示，程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“mMODn”表示m除以n的余数），若输入的m，n分别为2016，612，则输出的m=（ ）| A． | 0 | B． | 36 | C． | 72 | D． | 180 |
7．已知α为锐角，且$cos（{α+\frac{π}{4}}）=\frac{3}{5}$，则cos2α=（ ）
| A． | $\frac{24}{25}$ | B． | $\frac{7}{25}$ | C． | $-\frac{24}{25}$ | D． | $±\frac{24}{25}$ |
4．若x，y∈R+，且x+3y=5xy，则3x+4y的最小值是（ ）
| A． | 5 | B． | $\frac{24}{5}$ | C． | $\frac{{2\sqrt{3}}}{5}$ | D． | $\frac{19}{5}$ |
5．箱中装有标号为1，2，3，4，5，6且大小相同的6个球，从箱中一次摸出两个球，记下号码并放回，如果两球号码之积是4的倍数，则获奖，现有4人参与摸奖，恰好有3人获奖的概率是（ ）
| A． | $\frac{16}{625}$ | B． | $\frac{96}{625}$ | C． | $\frac{624}{625}$ | D． | $\frac{4}{625}$ |