题目内容
幂函数f（x）=xa图象过（2，
），则f（2）= ．
| 1 |
| 2 |
考点：幂函数的概念、解析式、定义域、值域
专题：函数的性质及应用
分析：根据幂函数f（x）的图象过（2，
），得出x=2时，f（2）的值．
| 1 |
| 2 |
解答：
解：∵幂函数f（x）=xa图象过（2，
），
即x=2时，f（2）=
．
故答案为：
．
| 1 |
| 2 |
即x=2时，f（2）=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查了函数的图象与性质的应用问题，解题时应利用函数的图象上的点与函数值的对应关系进行解答，是基础题．
练习册系列答案
相关题目
命题“若?x∈D，f（-x）=f（x），则函数y=f（x）（x∈D）是偶函数”的逆否命题是（ ）
| A、若函数y=f（x）（x∈D）不是偶函数，则?x∈D，f（-x）≠f（x） |
| B、若函数y=f（x）（x∈D）不是偶函数，则?x∈D，f（-x）≠f（x） |
| C、若?x∈D，f（-x）≠f（x），则函数y=f（x）（x∈D）不是偶函数 |
| D、若?x∈D，f（-x）≠f（x），则函数y=f（x）（x∈D）不是偶函数 |
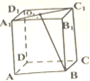如图，在长方体ABCD-A1B1C1D1中，A1C1的中点为O1，AB=BC=2，AA1=3，求异面直线BO1与A1D1所成角的余弦值．