题目内容
已知 函数f(x) =
函数f(x) = 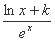 (k为常数,e=2.71828……是自然对数的底数),曲线y= f(x)在点(1,f(1))处的切线与x轴平行.
(k为常数,e=2.71828……是自然对数的底数),曲线y= f(x)在点(1,f(1))处的切线与x轴平行.
(Ⅰ)求k的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=(x2+x) 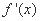 ,其中
,其中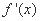 为f(x)的导函数,证明:对任意x>0,
为f(x)的导函数,证明:对任意x>0,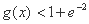 .
.
解析:由f(x) = 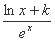 可得
可得
 ,而
,而 ,即
,即 ,解得
,解得 ;
;
(Ⅱ)
 ,令
,令 可得
可得 ,
,
当 时,
时, ;当
;当 时,
时, .
.
于是 在区间
在区间 内为增函数;在
内为增函数;在 内为减函数.
内为减函数.
简证(Ⅲ) ,
,
当 时,
时,  ,
, .
.
当
 时,要证
时,要证 .
.
只需证 ,然后构造函数即可证明.
,然后构造函数即可证明.

练习册系列答案
相关题目
 的底面是矩形,
的底面是矩形, ⊥底面
⊥底面 ,
, ,
, ,
,
 为
为 的中点.(1)求异面直线
的中点.(1)求异面直线 与平面
与平面 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.
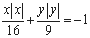 的曲线即为函数
的曲线即为函数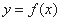 的图像,对于函数
的图像,对于函数 在R上单调递减;②函数
在R上单调递减;②函数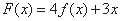 不存在零点;③函数
不存在零点;③函数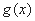 和
和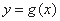 的图像就是方程
的图像就是方程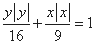 确定的曲线.其中所有正确的命题序号是 ( )
确定的曲线.其中所有正确的命题序号是 ( ) ,
, 则
则 的元素个数为( )
的元素个数为( ) 的定义域为 ( )
的定义域为 ( ) B.
B.  C.
C.  D.
D. 
 则满足f(x)≤2的x的取值范围是( )
则满足f(x)≤2的x的取值范围是( ) ) D.[0,+
) D.[0,+ .
.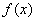 的单调区间与极值;
的单调区间与极值; ,使得对任意的
,使得对任意的 ,当
,当 时恒有
时恒有 成立.若存在,求
成立.若存在,求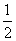 .
.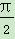 ,且sin α=
,且sin α=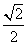 ,求f(α)的值;
,求f(α)的值;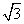 ≈1.73)
≈1.73)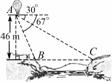 图13
图13