题目内容
已知函数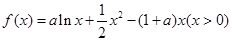 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若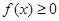 在
在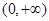 内恒成立,求实数
内恒成立,求实数 的取值范围.
的取值范围.
(Ⅰ)当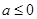 时,
时, 在
在 单调递减,在
单调递减,在 上单调递增;
上单调递增;
当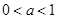 时,
时, 在
在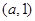 单调递减,在
单调递减,在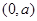 ,
, 上单调递增;
上单调递增;
当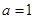 时,
时, 在
在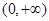 上单调递增;
上单调递增;
当 时,
时, 在
在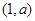 单调递减, 在
单调递减, 在 ,
,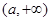 上单调递增;
上单调递增;
(Ⅱ)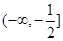
解析试题分析:(Ⅰ)利用导数的符号确定函数的单调区间。函数含有参数,故需要分情况讨论
(Ⅱ)思路一、一般地若任意 使得
使得 ,则
,则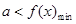 ;若任意
;若任意 使得
使得 ,则
,则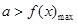 .由
.由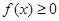 得:
得: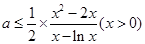 恒成立,所以
恒成立,所以 小于等于
小于等于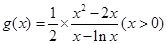 的最小值.
的最小值.
思路二、除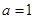 外,
外,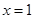 是
是 的一个极值点,故可首先考虑
的一个极值点,故可首先考虑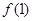 这个特殊值.由
这个特殊值.由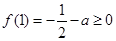 得:
得: 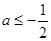 ,这样只需考虑
,这样只需考虑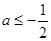 时
时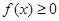 在
在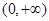 内是否恒成立.这是本题的特点,需要仔细观察、分析.若发现其特点,则运算大大简化.所以这个题有较好的区分度.
内是否恒成立.这是本题的特点,需要仔细观察、分析.若发现其特点,则运算大大简化.所以这个题有较好的区分度.
试题解析:(Ⅰ)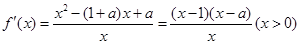
当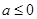 时,
时, 在
在 单调递减,在
单调递减,在 上单调递增;
上单调递增;
当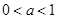 时,
时, 在
在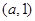 单调递减,在
单调递减,在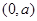 ,
, 上单调递增;
上单调递增;
当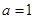 时,
时, 在
在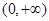 上单调递增;
上单调递增;
当 时,
时, 在
在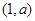 单调递减, 在
单调递减, 在 ,
,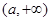 上单调递增.
上单调递增.
(Ⅱ)法一、由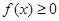 得:
得: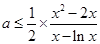
令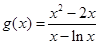 ,则
,则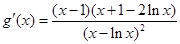
令 ,则
,则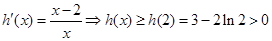 即
即
所以由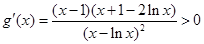 得
得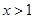
所以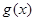 在
在 内单调递减,在
内单调递减,在 内单调递增.所以
内单调递增.所以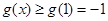
从而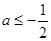
法二、由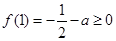 得:
得: 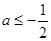
又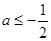 时,
时,  在
在 单调递减,在
单调递减,在 上单调递增
上单调递增
所以即: 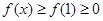
所以若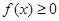 在
在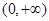 内恒成立,实数
内恒成立,实数 的取值范围为
的取值范围为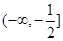 .
.
考点:本题考查函数的导数、导数的应用及不等关系.

练习册系列答案
相关题目
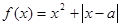 (
(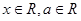 ).
). 的奇偶性;
的奇偶性;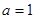 时,求
时,求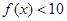 对
对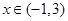 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 是定义在
是定义在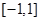 上的奇函数,且
上的奇函数,且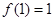 ,若
,若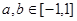 ,
,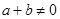 有
有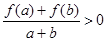 恒成立.
恒成立.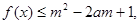 对所有
对所有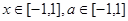 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。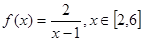 ,试判断此函数
,试判断此函数 在
在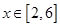 上的单调性,并求此函数
上的单调性,并求此函数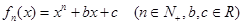
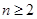 ,
,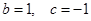 ,证明:
,证明: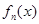 在区间
在区间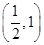 内存在唯一的零点;
内存在唯一的零点;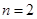 ,若对任意
,若对任意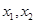
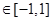 ,有
,有 ,求
,求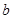 的取值范围;
的取值范围;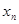 是
是 在
在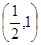 内的零点,判断数列
内的零点,判断数列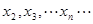 的增减性.
的增减性. ,函数
,函数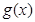
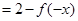 .
.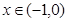 时,
时,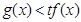 恒成立,求实数
恒成立,求实数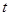 的最大值.
的最大值. (
( 为常数).
为常数).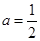 时,求
时,求 的单调递减区间;
的单调递减区间;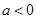 ,且对任意的
,且对任意的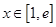 ,
,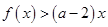 恒成立,求实数
恒成立,求实数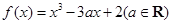 .
. 的单调递增区间;
的单调递增区间;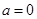 时,在曲线
时,在曲线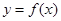 上是否存在两点
上是否存在两点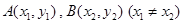 ,使得曲线在
,使得曲线在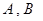 两点处的切线均与直线
两点处的切线均与直线 交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;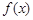 在区间
在区间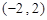 存在最大值
存在最大值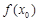 ,试构造一个函数
,试构造一个函数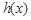 ,使得
,使得 ,且
,且 ;②当
;②当 时,
时, ;③在
;③在 中使
中使 值,从小到大组成等差数列.(只要写出函数
值,从小到大组成等差数列.(只要写出函数 ,
, .
.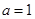 ,求函数
,求函数 的极值;
的极值;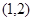 上有极值,求
上有极值,求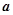 的取值范围.
的取值范围.