题目内容
设函数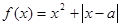 (
(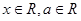 ).
).
(1)讨论 的奇偶性;
的奇偶性;
(2)当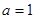 时,求
时,求 的单调区间;
的单调区间;
(3)若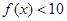 对
对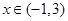 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)当a=0时,f(x)为偶函数;当a≠0时,f(x)为非奇非偶函数;
(2)(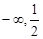 )为减区间,[
)为减区间,[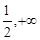 )为增区间;(3)
)为增区间;(3)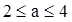
解析试题分析:(1)当a=0时,f(x)为偶函数;当a≠0时,f(x)为非奇非偶函数;
(2)a=1时,f(x)=x2+|x-1|=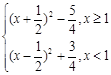 ,再进行配方,利用函数的图象,确定函数的单调区间;(3)f(x)=x2+|x-a|<10对x∈(-1,3)恒成立,等价于x2-10<x-a<10-x2,分离参数可得
,再进行配方,利用函数的图象,确定函数的单调区间;(3)f(x)=x2+|x-a|<10对x∈(-1,3)恒成立,等价于x2-10<x-a<10-x2,分离参数可得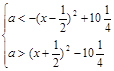 ,对x∈(-1,3)恒成立,从而可求实数a的取值范围.
,对x∈(-1,3)恒成立,从而可求实数a的取值范围.
试题解析:(1)若a=0时,f(x)为偶函数,若a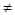 0时,f(x)为非奇非偶函数 3分
0时,f(x)为非奇非偶函数 3分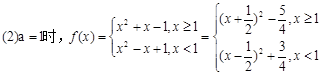
得f(x):(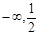 )为减区间,[
)为减区间,[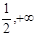 )为增区间 7分
)为增区间 7分
(3)f(x)=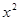 +|x-a|<10对
+|x-a|<10对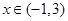 恒成立,
恒成立,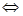
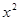 -10<x-a<10 -
-10<x-a<10 -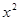
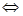
 14分
14分
考点:1.函数的单调性及单调区间;2.函数奇偶性的判断;3.函数恒成立问题

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
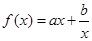 ,且
,且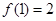 ,
,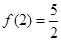 (1)判断函数
(1)判断函数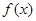 的奇偶性;(2)判断
的奇偶性;(2)判断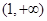 上的单调性并加以证明.
上的单调性并加以证明.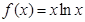 .
. 的单调区间和极值;
的单调区间和极值;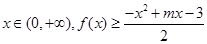 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.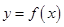 和
和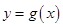 的图象关于
的图象关于 轴对称,且
轴对称,且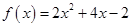 .
.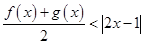 .
.
 在[0,+∞)上是减函数,试比较
在[0,+∞)上是减函数,试比较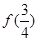 与
与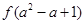 的大小.
的大小.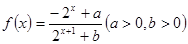 .
.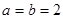 时,证明:函数
时,证明:函数 不是奇函数;
不是奇函数;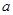 与
与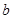 的值;
的值;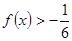 的解集.
的解集.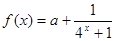 是奇函数.
是奇函数. 的单调性并证明;
的单调性并证明;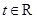 ,不等式
,不等式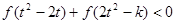 恒成立,求
恒成立,求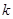 的取值范围.
的取值范围.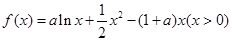 .
. 的单调区间;
的单调区间;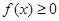 在
在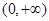 内恒成立,求实数
内恒成立,求实数 的取值范围.
的取值范围.