题目内容
已知函数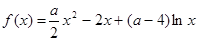 ,
, .
.
(Ⅰ)若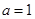 ,求函数
,求函数 的极值;
的极值;
(Ⅱ)若函数 在
在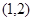 上有极值,求
上有极值,求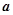 的取值范围.
的取值范围.
(1)函数有极小值 ,无极大值
,无极大值
(2)
解析试题分析:解:(Ⅰ)若 ,则
,则 .
. . …2分
. …2分
当 时,
时, ;当
;当 时,
时, . …4分
. …4分
所以函数有极小值 ,无极大值. …6分
,无极大值. …6分
(II) .
.
记 .
.
若 在
在 上有极值,则
上有极值,则 有两个不等根且在
有两个不等根且在 上有根. …8分
上有根. …8分
由 得
得 ,
,
所以 . …10分
. …10分
因为 ,所以
,所以 .
.
经检验当 时,方程
时,方程 无重根.
无重根.
故函数 在
在 上有极值时
上有极值时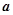 的取值范围为
的取值范围为 . …14分
. …14分
考点:导数的运用
点评:主要是运用导数研究函数的单调性以及函数极值问题的运用,属于中档题。

练习册系列答案
相关题目
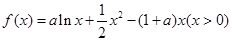 .
. 的单调区间;
的单调区间;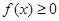 在
在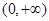 内恒成立,求实数
内恒成立,求实数 的取值范围.
的取值范围. ,
, ,
, 为奇函数,求
为奇函数,求 的值;
的值; 上是减函数;
上是减函数; 上的最小值.
上的最小值.  ,其中
,其中 ,区间
,区间 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 ;
; ,当
,当 时,求
时,求 (
( 为常数),且
为常数),且 在点
在点 处的切线平行于
处的切线平行于 轴.
轴. .
. 的单调区间;
的单调区间; 时
时 恒成立,求
恒成立,求 的取值范围。
的取值范围。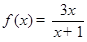 ,求
,求 在区间[2,5]上的最大值和最小值
在区间[2,5]上的最大值和最小值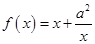 ,
,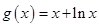 ,其中
,其中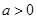 .
. 是函数
是函数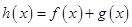 的极值点,求实数
的极值点,求实数 的值;
的值;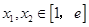 (
(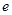 为自然对数的底数)都有
为自然对数的底数)都有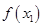 ≥
≥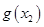 成立,求实数
成立,求实数
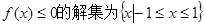 ,求实数b,c的值;
,求实数b,c的值;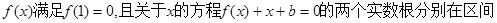
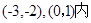 求实数
求实数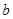 的取值范围.
的取值范围.