题目内容
4．当x＞1时，2log2x+$\frac{1}{lo{g}_{2}x}$的最小值为2$\sqrt{2}$．分析 直接利用基本不等式求解表达式的最小值即可．
解答 解：当x＞1时，log2x＞0，
2log2x+$\frac{1}{lo{g}_{2}x}$≥2$\sqrt{2lo{g}_{2}x•\frac{1}{lo{g}_{2}x}}$=2$\sqrt{2}$，
当且仅当log2x=$\frac{\sqrt{2}}{2}$时取等号．
故答案为：2$\sqrt{2}$．
点评 本题考查基本不等式的应用，函数的最值的求法，是基础题．
练习册系列答案
相关题目
15．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{4}$，$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$（λ∈R），其中$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为不共线的单位向量，若对符合上述条件的任意向量$\overrightarrow{a}$，$\overrightarrow{b}$恒有|$\overrightarrow{a}$-$\overrightarrow{b}$|≥$\frac{\sqrt{3}}{4}$，则$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$夹角的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5}{6}π$ |
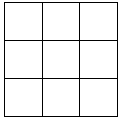将4个红球与2个蓝球（这些球只有颜色不同，其他完全相同）放入一个3×3的格子状木柜里（如图所示），每个格至多放一个球，则“所有红球均不位于相邻格子”的放法共有（ ）种．