题目内容
12．
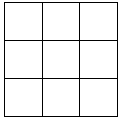将4个红球与2个蓝球（这些球只有颜色不同，其他完全相同）放入一个3×3的格子状木柜里（如图所示），每个格至多放一个球，则“所有红球均不位于相邻格子”的放法共有（ ）种．| A． | 30 | B． | 36 | C． | 60 | D． | 72 |
分析 对红球的位置分类讨论：第一类，当4个红球在4个顶角的位置时，蓝球放在剩下5个格种任选两个；第二类，当有一个红球再最中间时，其它三个红球只能放在顶角位置，蓝球放在剩下5个格种任选两个；第三类，当4个红球放在每外围三个格的中间时，蓝球放在剩下5个格种任选两个，即可得出．
解答 解：第一类，当4个红球在4个顶角的位置时，蓝球放在剩下5个格种任选两个，故有C52=10种，如图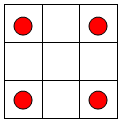
第二类，当有一个红球再最中间时，其它三个红球只能放在顶角位置，有出C43=4种，蓝球放在剩下5个格种任选两个，C43C52=40种，如图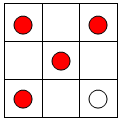
第三类，当4个红球放在每外围三个格的中间时，蓝球在剩下5个格种任选两个有C52=10种，如图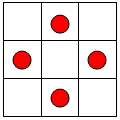
根据分类计数原理，故有10+40+10=60．
故选：C．
点评 本题主要考查了分类计数原理，关键是如何分类，属于中档题．
练习册系列答案
相关题目
2．对于两个平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，定义它们的一种运算：$\overrightarrow{a}$?$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|sinθ（其中θ为向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角），则关于这种运算的以下结论中，不恒成立的是（ ）
| A． | $\overrightarrow{a}$?$\overrightarrow{b}$=$\overrightarrow{b}$?$\overrightarrow{a}$ | |
| B． | 若$\overrightarrow{a}$?$\overrightarrow{b}$=0，则$\overrightarrow{a}$$∥\overrightarrow{b}$ | |
| C． | （$\overrightarrow{a}$+$\overrightarrow{b}$）?$\overrightarrow{c}$=$\overrightarrow{a}$?$\overrightarrow{c}$+$\overrightarrow{b}$?$\overrightarrow{c}$ | |
| D． | 若$\overrightarrow{a}$=（x1，y1），$\overrightarrow{b}$=（x2，y2），则$\overrightarrow{a}$?$\overrightarrow{b}$=|x1y2-x2y1| |