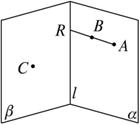
题目内容
设平面α∥平面β,A,C∈α,B,D∈β,直线AB与CD交于点S,且点S位于平面α,β之间,AS=8,BS=6,CS=12,则SD=
9
9
.分析:根据题意做出符合题意的图形(如下图)然后根据图形再结合线面平行的性质定理可得AC∥DB故△ASC∽△DSB故可得
=
,再结合条件AS=1,BS=2,CD=6即可求出SD的值.
| AS |
| SB |
| CS |
| SD |
解答: 解:根据题意做出如下图形:
解:根据题意做出如下图形:
∵AB,CD交于S点
∴三点确定一平面,所以设ASC平面为n,于是有n交α于AC,交β于DB,
∵α,β平行
∴AC∥DB
∴△ASC∽△DSB
∴
=
∵AS=8,BS=6,CS=12
∴
=
∴SD=9.
故答案为:9.
 解:根据题意做出如下图形:
解:根据题意做出如下图形:∵AB,CD交于S点
∴三点确定一平面,所以设ASC平面为n,于是有n交α于AC,交β于DB,
∵α,β平行
∴AC∥DB
∴△ASC∽△DSB
∴
| AS |
| SB |
| CS |
| SD |
∵AS=8,BS=6,CS=12
∴
| 8 |
| 6 |
| 12 |
| SD |
∴SD=9.
故答案为:9.
点评:本题主要考查利用平面图形的性质求空间中的线段长.解题的关键是首先正确的做出符合题意的图形然后利用线面平行的性质定理将空间中的距离转化为两个相似三角形ASC,SBD中的线段长即将空间中的距离转化为平面图形中的线段长!

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目