题目内容
16．已知数列{an}的前n项和为Sn=2n2-n+1，则a4+a5+a6=（ ）| A． | 67 | B． | 51 | C． | 38 | D． | 16 |
分析 直接利用数列求和公式，化简求解即可．
解答 解：数列{an}的前n项和为Sn=2n2-n+1，
则a4+a5+a6=S6-S3=（2×62-6+1）-（2×33-3+1）
=67-16=51．
故选：B．
点评 本题考查数列与函数的应用，数列的函数特征，考查计算能力．
练习册系列答案
相关题目
7．
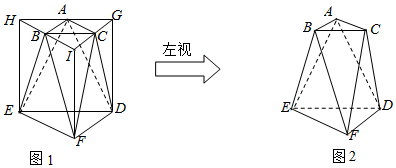如图，把侧棱与底面垂直，且底面边长和侧棱长都等于的三棱柱截去三个角（如图1所示，A，B，C分别是△GHI三边的中点）后得到的几何体如图2所示，则该几何体按图中所示方向的左视图（侧视图）为（ ）
如图，把侧棱与底面垂直，且底面边长和侧棱长都等于的三棱柱截去三个角（如图1所示，A，B，C分别是△GHI三边的中点）后得到的几何体如图2所示，则该几何体按图中所示方向的左视图（侧视图）为（ ）| A． |  | B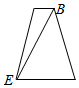． |  | C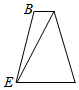． |  | D． |  |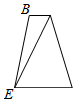
4．在△ABC中，已知sin（A-B）cosB+cos（A-B）sinB≥1，则△ABC是（ ）
| A． | 直角三角形 | B． | 锐角三角形 | C． | 钝角三角形 | D． | 等边三角形 |
8．某公司的班车在7：00，8：00，8：30发车，小明在7：50至8：30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |