题目内容
已知函数f(x)＝ax2＋blnx在x＝1处有极值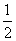
.
(1)求a，b的值；
(2)求函数y＝f(x)的单调区间．
解 (1)f′(x)＝2ax＋
.又f(x)在x＝1处有极值.
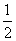得
解之得a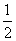＝，b＝－1.
(2)由(1)可知f(x)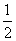＝x2－lnx，其定义域是(0，＋∞)，
且f′(x)＝x－
＝
.
由f′(x)<0，得0<x<1；
由f′(x)>0，得x>1.
所以函数y＝f(x)的单调减区间是(0,1)，单调增区间是(1，＋∞)．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
是奇函数，且
，则nm的取值范围为________．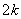
)处的切线与x轴的交点的横坐标为ak＋1，其中k∈N*，若a1＝16，则a1＋a3＋a5的值是________．
，e<a<b，则( )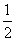
x2－lnx的最小值为________．
，f(2)的大小关系为________．
，α∈
，则tan
的值是________．