题目内容
抛物线y=x2-（2a-1）x+a2-1与x轴的交点在y轴同一侧的一个充分非必要条件为 ．
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：抛物线y=x2-（2a-1）x+a2-1与x轴的交点在y轴同一侧的一个充分非必要条件为
．解出即可．
|
解答：
解：抛物线y=x2-（2a-1）x+a2-1与x轴的交点在y轴同一侧的一个充分非必要条件为
．
解得1＜a≤
．
故答案为：1＜a≤
．
|
解得1＜a≤
| 5 |
| 4 |
故答案为：1＜a≤
| 5 |
| 4 |
点评：本题考查了二次函数的性质、充要条件的判定，属于中档题．
练习册系列答案
相关题目
已知数列{an}满足：a1=1，
=
，n∈N*，{an}的前项和为Sn，则（ ）
| 1 |
| an+1 |
| 1 |
| 2an |
A、Sn=2-（
| ||
B、Sn=2-（
| ||
| C、Sn=2n-1 | ||
| D、Sn=2n-1-1 |
已知函数f（x）=ax3+bx2+cx+d（a≠0）的对称中心为M（x0，y0），记函数f（x）的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x0）=0．若函数f（x）=x3-3x2，则可求出f（
）+f（
）+f（
）+…+f（
）+f（
）的值为（ ）
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4028 |
| 2015 |
| 4029 |
| 2015 |
| A、4029 | B、-4029 |
| C、8058 | D、-8058 |
“0＜k＜9”是“曲线
-
=1与曲线
-
=1的焦距相同”的（ ）
| x2 |
| 25 |
| y2 |
| 9-k |
| x2 |
| 25-k |
| y2 |
| 9 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
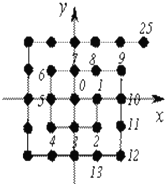将平面直角坐标系中的格点（横、纵坐标均为整数的点）按如下规则标上数字标签：原点处标0，点（1，0）处标1，点（1，-1）处标2，点（0，-1）处标3，点（-1，-1）处标4，…，点（0，1）处标7，…，依此类推，则标签20152的格点的坐标为（ ）| A、（1008，1007） |
| B、（1007，1006） |
| C、（1007，1005） |
| D、（1006，1005） |