题目内容
已知椭圆中心在原点,焦点在x轴上,长轴长等于12,离心率为
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)在椭圆上任取一点P,过P点做y轴垂线段PQ,Q为垂足,当P在椭圆上运动时,求线段PQ的中点M的轨迹方程.
| 1 |
| 3 |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)在椭圆上任取一点P,过P点做y轴垂线段PQ,Q为垂足,当P在椭圆上运动时,求线段PQ的中点M的轨迹方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)依题意,可求得椭圆的半长轴a=6,半焦距c=2,从而可求得半短轴b,于是可得椭圆的方程.
(Ⅱ)设线段PQ的中点为M(x,y),点P的坐标是(x0,y0),则
,由点P在椭圆上,能求出线段PQ中点M的轨迹方程.
(Ⅱ)设线段PQ的中点为M(x,y),点P的坐标是(x0,y0),则
|
解答:
解:(Ⅰ)由题意知,2a=12,
=
,故a=6,c=2,
∴b2=a2-c2=32,
故所求椭圆的方程为:
+
=1.
(Ⅱ)设线段PQ的中点为M(x,y),
点P的坐标是(x0,y0),
那么:
,
由点P在椭圆上,得
+
=1,即
+
=1,
∴线段PQ中点M的轨迹方程是
+
=1.
| c |
| a |
| 1 |
| 3 |
∴b2=a2-c2=32,
故所求椭圆的方程为:
| x2 |
| 36 |
| y2 |
| 32 |
(Ⅱ)设线段PQ的中点为M(x,y),
点P的坐标是(x0,y0),
那么:
|
由点P在椭圆上,得
| 4x2 |
| 36 |
| y2 |
| 32 |
| y2 |
| 32 |
| x2 |
| 9 |
∴线段PQ中点M的轨迹方程是
| y2 |
| 32 |
| x2 |
| 9 |
点评:本题考查椭圆方程的求法和求线段PQ的中点M的轨迹方程.主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
在区间[-2,3]上任取一个数a,则函数f(x)=x2-2ax+a+2有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
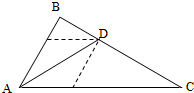 如图,△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且
如图,△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且| AD |
| 1 |
| 4 |
| AC |
| AB |
A、2
| ||
B、3
| ||
C、4
| ||
D、5
|
 如图,F1(-c,0),F2(c,0)分别是双曲线C:
如图,F1(-c,0),F2(c,0)分别是双曲线C: