题目内容
(2012•安徽模拟)若函数f(x)在R上可导,且满足f(x)>xf′(x),则( )
A.3f(1)>f(3) B.3f(1)<f(3) C.3f(1)=f(3) D.f(1)=f(3)
A
【解析】
试题分析:根据条件f(x)>xf′(x)可构造函数g(x)= ,然后得到函数的单调性,从而得到所求.
,然后得到函数的单调性,从而得到所求.
【解析】
设g(x)= ,g′(x)=
,g′(x)=
∵f(x)>xf′(x),
∴g′(x)= <0
<0
即g(x)在(0,+∞)上单调递减函数
∴ 即3f(1)>f(3)
即3f(1)>f(3)
故选A.

练习册系列答案
相关题目
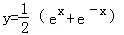 的导数是( )
的导数是( )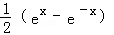 B.
B.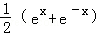 C.ex﹣e﹣x D.ex+e﹣x
C.ex﹣e﹣x D.ex+e﹣x
 B.
B. C.
C. D.
D.
 = .
= . ,
, ,且
,且 ,
, ,则
,则 的值是( )
的值是( ) (B)
(B) (C)
(C) 或
或 (D)
(D) 或
或