题目内容
1.已知${(\sqrt{x}-\frac{2}{x^2})^n}\;(n∈{N_+})$的展开式中第五项系数与第三项的系数的比值是10.(1)求展开式的各项系数和及二项式系数和;
(2)求展开式中x-1的项的系数;
(3)求展开式中系数绝对值最大的项.
分析 通过展开式中第五项的系数与第三项的系数的比是10:1得到n值,然后求要求的特征项.
解答 解:(1)由题意,第五项系数和第三项系数比值是10,即$\frac{{C}_{n}^{4}•(-2)^{4}}{{C}_{n}^{2}•(-2)^{2}}$=10,
化简得n2-5n-24=0,解得n=8或n=-3(舍去).
(1)令x=1得各项系数和为(1-2)8=1;二项式系数和28=256;
(2)通项公式为Tr+1=$(-2)^{r}{C}_{8}^{r}{x}^{4-\frac{5r}{2}}$,
令4-$\frac{5r}{2}$=-1,则r=2,
所以展开式中含x-1的项的系数为112;
(3)由2r-1C8r-1≥2rC8r,2r-1C8r-1≥2r-2C8r-2,解得r=5或6,
∴展开式中系数绝对值最大的项为T6=-1792${x}^{-\frac{17}{2}}$,T7=1792x11.
点评 本题考查了二项式定理的运用;关键是利用已知求出指数后,找出二项式的展开式通项,根据x的指数求特征项.

练习册系列答案
相关题目
9.函数f(x)=cos(x+φ)(0≤φ≤π)的定义域为R,若f(x)为奇函数,则φ=( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
16.定义为n个正数p1,p2,p3…pn的“均倒数”,若已知数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$,又${b_n}=\frac{{{a_n}+1}}{4}$,则$\frac{1}{{{b_1}{b_2}}}+\frac{1}{{{b_2}{b_3}}}+\frac{1}{{{b_3}{b_4}}}+$…$+\frac{1}{{{b_{2015}}{b_{2016}}}}$=( )
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
6.下列叙述正确的是( )
| A. | 第一或第二象限的角都可作为三角形的内角 | |
| B. | 钝角比第三象限的角小 | |
| C. | 第四象限的角一定是负角 | |
| D. | 始边相同而终边不同的角一定不相等 |
13.某大型汽车城为了了解销售单价(单位:万元)在[8,20]内的轿车的销售情况,从2016年上半年已经销售的轿车中随机抽取100辆,按其销售单价分成6组,制成如下的频数分布表.
已知样本中销售单价在[14,16)内的轿车数是销售单价在[18,20]内的轿车数的2倍.
(1)用分层抽样的方法从单价在[8,10),[10,12)和[18,20]内的轿车中共抽取6辆,求销售单价在[18,20]内的轿车数;
(2)在(1)中抽出的6辆轿车中任取2辆,求至少有1辆轿车的销售单价在[18,20]内的概率.
| 销售单价/万元 | [8,10) | [10,12) | [12,14) | [14,16) | [16,18) | [18,20] |
| 频数/辆 | 5 | 10 | 20 | a | 20 | b |
(1)用分层抽样的方法从单价在[8,10),[10,12)和[18,20]内的轿车中共抽取6辆,求销售单价在[18,20]内的轿车数;
(2)在(1)中抽出的6辆轿车中任取2辆,求至少有1辆轿车的销售单价在[18,20]内的概率.
13.了研究某种细菌在特定环境下随时间变化的繁殖情况,得如下实验数据:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,预测t=8时,细菌繁殖个数.
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 2.5 | 3 | 4 | 4.5 | 6 |
(2)利用(1)中的回归方程,预测t=8时,细菌繁殖个数.

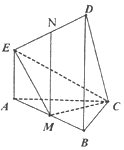 如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.
如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.