题目内容
20.下列函数中,最小正周期为π的偶函数是( )| A. | y=sin2x+cos2x | B. | $y=cos(2x+\frac{π}{2})$ | C. | y=cos(2x-1) | D. | y=cos2x |
分析 由条件利用三角函数的周期性和奇偶性,得出结论.
解答 解:由于y=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),不是偶函数,故排除A;
由于y=cos(2x+$\frac{π}{2}$)=-sin2x,是奇函数,故排除B;
由于y=cos(2x-1)是非奇非偶函数,故排除C;
由于y=cos2x=$\frac{1+cos2x}{2}$是偶函数,且它的最小正周期为$\frac{2π}{2}$=π,故D满足条件,
故选:D.
点评 本题主要考查三角函数的周期性和奇偶性,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
10.已知函数f(x)是定义在R上的奇函数,且在区间[0,+∞)上是增函数,则不等式$\frac{|f(lnx)-f(ln\frac{1}{x})|}{2}$<f(1)的解集为( )
| A. | (0,$\frac{1}{e}$) | B. | (0,e) | C. | ($\frac{1}{e}$,e) | D. | (e,+∞) |
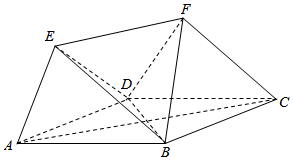 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.