题目内容

函数y=log2
x-1
x+1
的导数为（　　）
A、y′=
2ln2
x2-1
B、y′=
ln2
x2-1
C、y′=
2log2e
x2-1
D、y′=
2(x2-1)
ln2
考点：导数的运算
专题：计算题,导数的概念及应用
分析：由复合函数的导数求函数的导数．
解答： 解：∵y=log2
x-1
x+1
，
∴y′=
1
ln2
•
x+1
x-1
•
2
(x+1)2

=log2e•
2
x2-1

=
2log2e
x2-1
．
故选C．
点评：本题考查了函数的导数，属于基础题．
练习册系列答案
相关题目
sin（-
5π
3
）的值域为
 
．
设向量
a
=（1，-3），
b
=（-2，4），
c
=（1，5），若表示向量
a
、
b
、2
b
-
c
、
d
连接能构成四边形，则向量
d
为（
 
，
 
）．
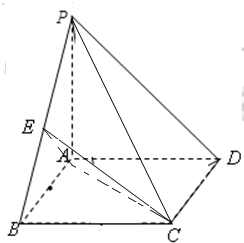如图，在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PA⊥底面，且AB=2，BC=1，PA=2，E为PD的中点．
（1）求证：面PAB⊥面PBC；
（2）求二面角E-AC-D的正切值．
在斜三棱柱ABC-A1B1C1中，侧面ACC1A1⊥面ABC，AA1=
2
，A1C=CA=AB=1，AB⊥AC，D为AA1中点．
（1）求证：CD⊥面ABB1A1；
（2）在侧棱BB1上确定一点E，使得二面角E-A1C1-A的大小为
π
3
．
已知函数y=2tan（2x+φ）是奇函数，则φ=
 
．
如图，在四棱锥P-ABCD中，PD⊥平面ABCD，四边形ABCD为菱形，E，F为PC的三等分点．
（Ⅰ）证明：AC⊥PB；
（Ⅱ）若PD=
3
，AD=2，∠BAD=60°，求二面角P-BC-A的大小；
（Ⅲ）在直线PB上是否存在一点G，使平面BDE∥平面AFG？说明理由．
在△ABC中，若a=2，b=1，∠B=45°，则此三角形有
 
个解．
已知A（-2，2）、B（2，1）、C（-2，-2），点P（x，y）在△ABC内部及其边界，若目标函数z=mx+ny的最大值不大于6，则mn的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网