题目内容
(本小题满分12分)已知椭圆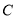 的中心在坐标原点,右焦点为
的中心在坐标原点,右焦点为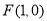 ,
,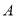 、
、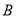 是椭圆
是椭圆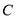 的左、右顶点,
的左、右顶点,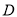 是椭圆
是椭圆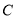 上异于
上异于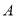 、
、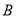 的动点,且
的动点,且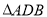 面积的最大值为
面积的最大值为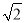 .
.
(1)求椭圆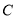 的方程;
的方程;
(2)是否存在一定点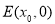 (
(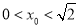 ),使得当过点
),使得当过点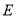 的直线
的直线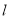 与曲线
与曲线 相交于
相交于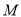 ,
,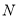 两点时,
两点时, 为定值?若存在,求出定点和定值;若不存在,请说明理由.
为定值?若存在,求出定点和定值;若不存在,请说明理由.
(1) ;(2)定点为
;(2)定点为 ,定值为
,定值为 .
.
【解析】
试题分析:(1)设椭圆 的标准方程为
的标准方程为 (
( ),由于
),由于 面积的最大值为
面积的最大值为 ,可得
,可得 ,联立
,联立 ,解得即可求出;
,解得即可求出;
(2)首先利用特殊位置探究得到定点的坐标与定值,再将直线方程与椭圆方程联立,利用韦达定理以及弦长的公式证明.
试题解析:(1)设椭圆的方程为 (
( ),由已知可得
),由已知可得 ①,
①,
∵ 为椭圆右焦点,∴
为椭圆右焦点,∴ ②,
②,
由①②可得 ,
, ,
,
 椭圆
椭圆 的方程为
的方程为 ;
;
(2)过点 取两条分别垂直于
取两条分别垂直于 轴和
轴和 轴的弦
轴的弦 ,
, ,
,
则 ,即
,即 ,
,
解得 ,∴
,∴ 若存在必为
若存在必为 ,定值为3,
,定值为3,
下证 满足题意,
满足题意,
设过点 的直线方程为
的直线方程为 ,代入
,代入 中得:
中得: ,设
,设 ,
, ,则
,则 ,
, ,
,

 ,综上得定点为
,综上得定点为 ,定值为3.
,定值为3.
考点:1.椭圆的标准方程及其性质;2.直线与椭圆相交弦长问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
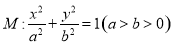 的离心率与双曲线
的离心率与双曲线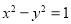 的离心率互为倒数,且椭圆的长轴长为
的离心率互为倒数,且椭圆的长轴长为 .
.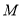 的方程;
的方程;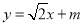 交椭圆
交椭圆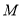 于
于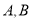 两点,
两点,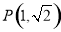 为椭圆
为椭圆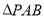 面积的最大值.
面积的最大值. ,
, 为虚数单位,
为虚数单位, ,若
,若 ,则复数
,则复数 的共轭复数
的共轭复数 的虚部是( )
的虚部是( ) B.
B. C.
C. D.
D.
 的图像向左平移
的图像向左平移 个单位后得到
个单位后得到 的图象,则
的图象,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 中,
中, ,
, ,
, (
( ),则数列
),则数列 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.2 C.
B.2 C. D.
D.
 成等差数列,则cos C的最小值是_____.
成等差数列,则cos C的最小值是_____.
 的最小正周期及值域;
的最小正周期及值域; 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,求
,求 的面积.
的面积.