题目内容
设椭圆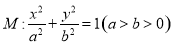 的离心率与双曲线
的离心率与双曲线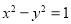 的离心率互为倒数,且椭圆的长轴长为
的离心率互为倒数,且椭圆的长轴长为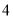 .
.
(Ⅰ)求椭圆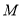 的方程;
的方程;
(Ⅱ)若直线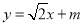 交椭圆
交椭圆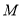 于
于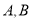 两点,
两点,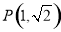 为椭圆
为椭圆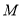 上一点,求
上一点,求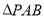 面积的最大值.
面积的最大值.
(Ⅰ)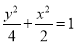 ;(Ⅱ)
;(Ⅱ) 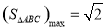 .
.
【解析】
试题分析:(Ⅰ)利用椭圆的离心率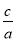 与双曲线的离心率
与双曲线的离心率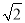 互为倒数,椭圆的长轴
互为倒数,椭圆的长轴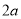 为
为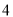 及
及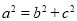 ,求得
,求得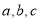 的值,进而求得椭圆的方程;(Ⅱ)将直线
的值,进而求得椭圆的方程;(Ⅱ)将直线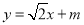 与(Ⅰ)求得的椭圆方程联立,利用韦达定理和
与(Ⅰ)求得的椭圆方程联立,利用韦达定理和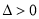 ,利用弦长公式及点
,利用弦长公式及点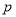 到直线
到直线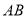 的距离,求得
的距离,求得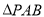 的面积,同时
的面积,同时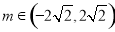 ,进而求得
,进而求得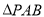 的面积的最大值.
的面积的最大值.
试题解析:(Ⅰ)双曲线的离心率为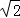 (1分),
(1分),
则椭圆的离心率为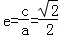 (2分), 2a=4, (3分)
(2分), 2a=4, (3分)
由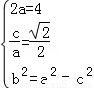
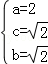 ,故椭圆M的方程为
,故椭圆M的方程为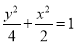 . (5分)
. (5分)
(Ⅱ)由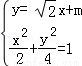 ,得
,得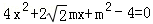 , (6分)
, (6分)
由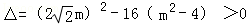 ,得﹣2
,得﹣2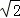 <m<2
<m<2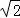
∵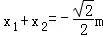 ,
,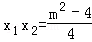 . (7分)
. (7分)
∴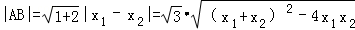 =
=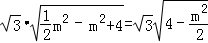 (9分)
(9分)
又P到AB的距离为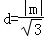 . (10分)
. (10分)
则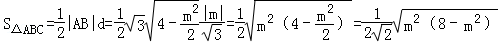
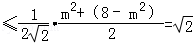 , (12分)
, (12分)
当且仅当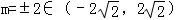 取等号 (13分)
取等号 (13分)
∴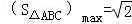 . (14分)
. (14分)
考点:1.椭圆的标准方程;2.韦达定理;3.弦长公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 到直线
到直线 的距离等于
的距离等于 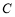 :
: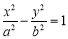
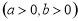 的右顶点为
的右顶点为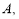
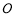 为坐标原点,以
为坐标原点,以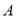 为圆心的圆与双曲线
为圆心的圆与双曲线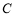 的某渐近线交于两点
的某渐近线交于两点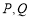 .若
.若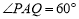 且
且 ,则双曲线
,则双曲线 的离心率为
的离心率为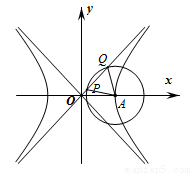
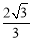 B.
B.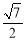 C.
C.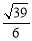 D.
D.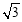
 满足:
满足: ,则
,则 的取值范围是 ,
的取值范围是 , 的最大值为 .
的最大值为 . ,那么
,那么  B.
B.
 D.
D.
 具有奇偶性,则
具有奇偶性,则 ,函数
,函数 的单调递减区间是 。
的单调递减区间是 。 是双曲线
是双曲线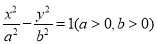 左支上一点,其右焦点为
左支上一点,其右焦点为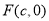 ,若
,若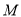 是线段
是线段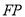 的中点且
的中点且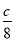 ,则双曲线离心率
,则双曲线离心率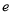 的取值范围是( )
的取值范围是( )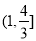 B.
B.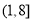 C.
C. D.
D.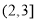
 则
则 时,
时, 表达式中的展开式中的常数项为 .(用数字作答)
表达式中的展开式中的常数项为 .(用数字作答)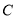 的中心在坐标原点,右焦点为
的中心在坐标原点,右焦点为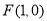 ,
,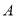 、
、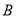 是椭圆
是椭圆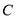 的左、右顶点,
的左、右顶点,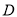 是椭圆
是椭圆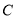 上异于
上异于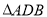 面积的最大值为
面积的最大值为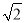 .
.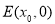 (
(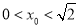 ),使得当过点
),使得当过点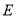 的直线
的直线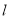 与曲线
与曲线 相交于
相交于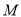 ,
,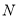 两点时,
两点时, 为定值?若存在,求出定点和定值;若不存在,请说明理由.
为定值?若存在,求出定点和定值;若不存在,请说明理由.