题目内容
已知抛物线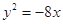 的准线过双曲线
的准线过双曲线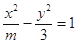 的右焦点,则双曲线的离心率为 .
的右焦点,则双曲线的离心率为 .
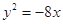 的准线过双曲线
的准线过双曲线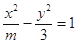 的右焦点,则双曲线的离心率为 .
的右焦点,则双曲线的离心率为 .2
试题分析:根据题意,由于抛物线
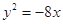 的准线x=2,过双曲线
的准线x=2,过双曲线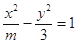 的右焦点(2,0),故可知m+3=4,m=1,故可知a=1,c=2,因此可知离心率为2,答案为2.
的右焦点(2,0),故可知m+3=4,m=1,故可知a=1,c=2,因此可知离心率为2,答案为2.点评:主要是考查了抛物线与双曲线的性质的运用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
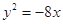 的准线过双曲线
的准线过双曲线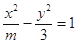 的右焦点,则双曲线的离心率为 .
的右焦点,则双曲线的离心率为 .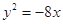 的准线x=2,过双曲线
的准线x=2,过双曲线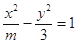 的右焦点(2,0),故可知m+3=4,m=1,故可知a=1,c=2,因此可知离心率为2,答案为2.
的右焦点(2,0),故可知m+3=4,m=1,故可知a=1,c=2,因此可知离心率为2,答案为2.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案