点P从点O出发.按逆时针方向沿周长为l的图形运动一周.O.P两点连线的距离y与点P走过的路程x的函数关系如图.那么点P所走的图形是( )A．B．C．D．题目和参考答案——青夏教育精英家教网——

题目内容

10．

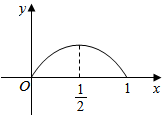点P从点O出发，按逆时针方向沿周长为l的图形运动一周，O，P两点连线的距离y与点P走过的路程x的函数关系如图，那么点P所走的图形是（　　）

A．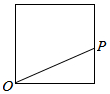

B．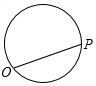

C．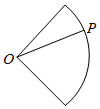

D．

分析根据O，P两点连线的距离y与点P走过的路程x的函数图象，由图象可知函数值随自变量的变化成轴对称性并且变化圆滑．由此即可排除A、C．D．

解答解：观察函数的运动图象，可以发现两个显著特点：
①点P运动到周长的一半时，OP最大；
②点P的运动图象是抛物线．
设点M为周长的一半，
A．当点P在线段OA上运动时，y=x，其图象是一条线段，不符合条件，

B．满足条件．

C．当点P在线段OA上运动时，y=x，其图象是一条线段，不符合条件，

D．OM≤OP，不符合条件①，并且OP的距离不是对称变化的，因此排除选项D．

故选：B．

点评本题考查函数图象的识别和判断，考查对于运动问题的深刻理解，解题关键是认真分析函数图象的特点．考查学生分析问题的能力．

练习册系列答案

魔力导学案系列答案

绩优中考系列答案

课堂追踪系列答案

活力英语课课练与单元检测系列答案

名师课时计划系列答案

全优AB卷系列答案

品优课堂系列答案

核心课堂武汉大学出版社系列答案

冠军练加考系列答案

考点集训与满分备考系列答案

相关题目

20．函数f（x）=x²+ax+b，其中a∈R，b∈R且（b+4）²-a²=4，已知对任意的x∈R不等式f（x）≥-2恒成立．
（1）求实数a，b的值；
（2）若函数g（x）=$\left\{\begin{array}{l}{f（x）+x+4，x＜f（x）}\\{f（x）-x，x≥f（x）}\end{array}\right.$，求g（x）的值域；
（3）是否存在实数m，n使得不等式m≤f（x）≤n的解集为[m，n]？若存在，求出m，n的值；若不存在，请说明理由．

1．设S_n为数列{a_n}的前n项和，且S_n=n²，数列{b_n}为等比数列．已知a₁b₁+a₂b₂+a₃b₃+…+a_nb_n=（n-1）•3ⁿ⁺¹+3．
（Ⅰ）求数列{a_n}，{b_n}的通项公式；
（Ⅱ）设（a_n+1）•log₃b_n+2•c_n=1，求证：数列{c_n}的前n项和T_n＜$\frac{3}{8}$．

18．在（x³+$\frac{1}{{x}^{2}}$）ⁿ的展开式中，若其展开式存在常数项，求n的最小正整数值．

5．已知函数f（x）=$\left\{\begin{array}{l}{x+1，0≤x＜1}\\{{2}^{x-1}-1，1≤x＜3}\end{array}\right.$，若存在m，n，当0≤m＜n＜3时，有f（m）=f（n），则nf（m）的取值范围是（　　）

[1，2log₂3+2）

[2，2log₂3+2）

15．已知数列{a_n}满足a₁=2，a_n+1-a_n=2（n∈N^*），数列{b_n}满足b₁=4，b₃=14，且数列{b_n-a_n}是各项均为正数的等比数列．
（Ⅰ）求数列{a_n}和{b_n}的通项公式；
（Ⅱ）令c_n=b_n-2n，求数列{$\frac{1}{{c}_{n}}$}的前n项和T_n．

2．已知复数z=2i（1-i）（i为虚数单位），z的共轭复数为$\overline{z}$，则$z+\overline{z}$=（　　）

19．若x，y满足约束条件$\left\{\begin{array}{l}x+y≥0\\ x-y≥-1\\ 2x-y≤2\end{array}\right.$，则目标函数z=x-2y的最小值是（　　）

20．已知f（α）=$\frac{tan（π-α）sin（-2π-α）cos（6π-α）}{sin（α+\frac{3}{2}π）cos（α-\frac{1}{2}π）}$
（1）化简f（α）；
（2）若sinα=-$\frac{2}{3}$，α∈[一π，-$\frac{π}{2}$]，求f（α）的值．