题目内容
20.已知f(α)=$\frac{tan(π-α)sin(-2π-α)cos(6π-α)}{sin(α+\frac{3}{2}π)cos(α-\frac{1}{2}π)}$(1)化简f(α);
(2)若sinα=-$\frac{2}{3}$,α∈[一π,-$\frac{π}{2}$],求f(α)的值.
分析 (1)使用诱导公式化简;
(2)根据α的范围求出cosα,代入化简后的f(α)解析式计算.
解答 解:(1)f(α)=$\frac{-tanαsin(-α)cos(-α)}{-cosαcos(\frac{π}{2}-α)}$=$\frac{tanαsinαcosα}{-cosαsinα}$=-tanα.
(2)∵sinα=-$\frac{2}{3}$,α∈[一π,-$\frac{π}{2}$],
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{\sqrt{5}}{3}$.
∴f(α)=-tanα=-$\frac{sinα}{cosα}$=-$\frac{2\sqrt{5}}{5}$.
点评 本题考查了三角函数的化简求值,需要熟练掌握三角函数公式,属于基础题.

练习册系列答案
相关题目
8.已知命题p:若方程x2+y2+2mx-2y+2m=0表示圆,则实数m≠1;
命题q:若以原点为对称中心,坐标轴为对称轴的双曲线的一条渐近线与直线2x-y+1=0平行,则双曲线的离心率等于$\sqrt{5}$,下列命题真确的是( )
命题q:若以原点为对称中心,坐标轴为对称轴的双曲线的一条渐近线与直线2x-y+1=0平行,则双曲线的离心率等于$\sqrt{5}$,下列命题真确的是( )
| A. | p∧q | B. | ¬p∨q | C. | p∧¬q | D. | ¬p∧¬q |
15.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+4x-1,x<0}\\{-{e}^{x}-x,x≥0}\end{array}\right.$若关于x的方程f(x)+m=0有3个实数根,则实数m的取值范围为( )
| A. | (1,3) | B. | (-3,-1) | C. | (1,5) | D. | (-5,-1) |
12.某小组共有13人,其中男生8人,女生5人,从中选出3人,要求至多有2名男生,则不同的选法共有( )
| A. | 140种 | B. | 150种 | C. | 220种 | D. | 230种 |
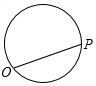
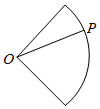
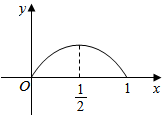 点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )
点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )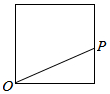

 在三棱锥A-BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2$\sqrt{3}$,AC=$\sqrt{6}$.
在三棱锥A-BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2$\sqrt{3}$,AC=$\sqrt{6}$.