题目内容
18．在（x3+$\frac{1}{{x}^{2}}$）n的展开式中，若其展开式存在常数项，求n的最小正整数值．分析 通项公式Tr+1=${∁}_{n}^{r}$x3n-5r，令3n-5r=0，可得n=$\frac{5}{3}$r，进而得出．
解答 解：通项公式Tr+1=${∁}_{n}^{r}$（x3）n-r$（\frac{1}{{x}^{2}}）^{r}$=${∁}_{n}^{r}$x3n-5r，
令用3n-5r=0，
可得n=$\frac{5}{3}$r≥$\frac{5}{3}×3$=5，
因此n的最小正整数值是5．
点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
9．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+ax，x≤0}\\{ln（x+1），x＞0}\end{array}\right.$，若对x∈R有|f（x）|≥-2x-4恒成立，则a的取值范围是（ ）
| A． | （-∞，0]∪[2，+∞） | B． | （-∞，-2]∪[0，+∞） | C． | [-2，+∞） | D． | [-2，0] |
13．设数列{an}的前n项和为Sn，若Sn+1，Sn，Sn+2成等差数列，且a2=-2，则a7=（ ）
| A． | 16 | B． | 32 | C． | 64 | D． | 128 |
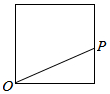
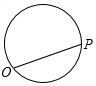
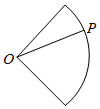
中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图（如图），其中上面的折线代表可能出现的最高气温，下面的折线代表可能出现的最低气温．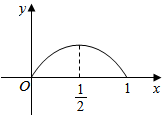
点P从点O出发，按逆时针方向沿周长为l的图形运动一周，O，P两点连线的距离y与点P走过的路程x的函数关系如图，那么点P所走的图形是（ ）
