题目内容
已知数列{an}的前n项和Sn满足Sn=2an+(-1)n,n≥1.求数列{an}的通项公式.
考点:数列的求和
专题:等差数列与等比数列
分析:利用递推式转化为等比数列,利用其通项公式即可得出.
解答:
解:∵Sn=2an+(-1)n,n≥1.
∴当n=1时,a1=2a1-1,解得a1=1.
当n≥2时,Sn-1=2an-1+(-1)n-1,
∴an=Sn-Sn-1=2an+(-1)n-2an-1-(-1)n-1,
化为an+
(-1)n=2[an-1+
(-1)n-1],
∴数列{an+
(-1)n}为等比数列,公比为2,首项为a1+
×(-1)=
.
∴an+
(-1)n=
×2n-1,
∴an=
.
∴当n=1时,a1=2a1-1,解得a1=1.
当n≥2时,Sn-1=2an-1+(-1)n-1,
∴an=Sn-Sn-1=2an+(-1)n-2an-1-(-1)n-1,
化为an+
| 2 |
| 3 |
| 2 |
| 3 |
∴数列{an+
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∴an+
| 2 |
| 3 |
| 1 |
| 3 |
∴an=
| 2n-1-2(-1)n |
| 3 |
点评:本题考查了递推式的应用、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
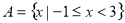 ,
,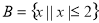 ,
,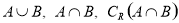 ;
;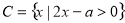 ,满足
,满足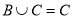 ,求实数
,求实数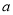 的取值范围。
的取值范围。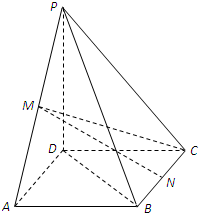 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=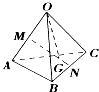 如图所示,已知空间四边形OABC,其对角线为OB,AC,M,N分别为OA,BC的中点,点G在线段MN上,且
如图所示,已知空间四边形OABC,其对角线为OB,AC,M,N分别为OA,BC的中点,点G在线段MN上,且