题目内容
18.如果点P(x,y)在平面区域$\left\{\begin{array}{l}2x-y+2≥0\\ x-2y+1≤0\\ x+y-2≤0\end{array}\right.$上,则x2+(y+1)2的最大值和最小值分别是( )| A. | 3,$\frac{3}{{\sqrt{5}}}$ | B. | 9,$\frac{9}{5}$ | C. | 9,2 | D. | 3,$\sqrt{2}$ |
分析 画出满足条件的平面区域,结合x2+(y+1)2的几何意义求出其最大值和最小值即可.
解答  解:如图,先作出点P(x,y)所在的平面区域:
解:如图,先作出点P(x,y)所在的平面区域:
x2+(y+1)2表示动点P到定点Q(0,-1)距离的平方,
当点P在(-1,0)时,|PQ|2=2,
而点Q到直线x-2y+1=0的距离的平方为$\frac{9}{5}<2$;
当点P在(0,2)时,离Q最远,|PQ|2=9;
因此x2+(y+1)2的最大值为9,最小值为$\frac{9}{5}$.
故选:B.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
相关题目
9.某校选定甲、乙、丙、丁、戊共5名教师到3个边远地区支教,每地至少1人,其中甲和乙一定不去同一地区,甲和丙必须去同一地区,则不同的选派方案共有( )
| A. | 27种 | B. | 30种 | C. | 33种 | D. | 36种 |
13.已知实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-3≤0}\\{y≥1}\end{array}\right.$若目标函数z=2x+y的最小值为a,最大值为b,则函数y=x-$\frac{4}{x}$在[a,b]上的值域为( )
| A. | (-∞,3) | B. | [3,$\frac{21}{5}$]. | C. | [-3,3] | D. | [5,+∞) |
3.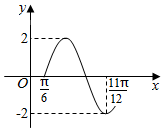 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )| A. | $({-\frac{π}{12}+2kπ,\frac{5π}{12}+2kπ})$,k∈Z | B. | $({-\frac{π}{12}+kπ,\frac{5π}{12}+kπ})$,k∈Z | ||
| C. | $({-\frac{π}{6}+2kπ,\frac{5π}{6}+2kπ})$,k∈Z | D. | $({-\frac{π}{6}+kπ,\frac{5π}{6}+kπ})$,k∈Z |
10.若函数f(x)=2sin(4x+φ)(φ<0)的图象关于直线x=$\frac{π}{24}$对称,则φ的最大值为( )
| A. | -$\frac{5π}{3}$ | B. | -$\frac{2π}{3}$ | C. | -$\frac{π}{6}$ | D. | -$\frac{5π}{6}$ |

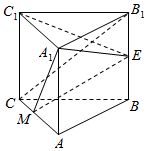 如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.
如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.