题目内容
3.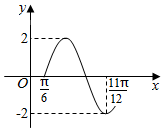 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )| A. | $({-\frac{π}{12}+2kπ,\frac{5π}{12}+2kπ})$,k∈Z | B. | $({-\frac{π}{12}+kπ,\frac{5π}{12}+kπ})$,k∈Z | ||
| C. | $({-\frac{π}{6}+2kπ,\frac{5π}{6}+2kπ})$,k∈Z | D. | $({-\frac{π}{6}+kπ,\frac{5π}{6}+kπ})$,k∈Z |
分析 由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.再根据正弦函数的单调性,得出结论.
解答 解:由图象可知A=2,$\frac{3}{4}T=\frac{11π}{12}-\frac{π}{6}=\frac{3π}{4}$,所以T=π,故ω=2.
由五点法作图可得2•$\frac{π}{6}$+φ=0,求得φ=-$\frac{π}{3}$,所以,$f(x)=2sin(2x-\frac{π}{3})$.
由$2x-\frac{π}{3}∈(2kπ-\frac{π}{2}\;,\;2kπ+\frac{π}{2})$(k∈Z),得$x∈(kπ-\frac{π}{12}\;,\;kπ+\frac{5π}{12})$(k∈Z).
所以f(x)的单增区间是$(kπ-\frac{π}{12}\;,\;kπ+\frac{5π}{12})$(k∈Z),
故选:B.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,正弦函数的单调性,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
13.在△ABC中,BC=7,cosA=$\frac{1}{5}$,sinC=$\frac{2\sqrt{6}}{7}$.若动点P满足$\overrightarrow{AP}$=$\frac{λ}{2}$$\overrightarrow{AB}$+(1-λ)$\overrightarrow{AC}$(λ∈R),则点的轨迹与直线AB,AC所围成的封闭区域的面积为( )π
| A. | $3\sqrt{6}$ | B. | $4\sqrt{6}$ | C. | $6\sqrt{6}$ | D. | 12$\sqrt{6}$ |
14.已知数列{an}是等比数列,若a2=2,a3=-4,则a5等于( )
| A. | 8 | B. | -8 | C. | 16 | D. | -16 |
18.如果点P(x,y)在平面区域$\left\{\begin{array}{l}2x-y+2≥0\\ x-2y+1≤0\\ x+y-2≤0\end{array}\right.$上,则x2+(y+1)2的最大值和最小值分别是( )
| A. | 3,$\frac{3}{{\sqrt{5}}}$ | B. | 9,$\frac{9}{5}$ | C. | 9,2 | D. | 3,$\sqrt{2}$ |
8.设i为虚数单位,(-3+4i)2=a+bi(a,b∈R),则|a+bi|等于( )
| A. | 5 | B. | 10 | C. | 25 | D. | 50 |
15.若${3^a}•{9^b}=\frac{1}{3}$,则下列等式正确的是( )
| A. | a+b=-1 | B. | a+b=1 | C. | a+2b=-1 | D. | a+2b=1 |
13.将除颜色外完全相同的一个白球、一个黄球、两个红球分给三个小朋友,且每个小朋友至少分得一个球的分法有 ( )种.
| A. | 15 | B. | 18 | C. | 21 | D. | 24 |