题目内容
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x= .
.
(1)求φ;
(2)求函数y=f(x)的单调增区间.
解析 (1)令2× +φ=kπ+
+φ=kπ+ ,k∈Z,
,k∈Z,
∴φ=kπ+ ,k∈Z,
,k∈Z,
又-π<φ<0,则- <k<-
<k<- ,k∈Z,
,k∈Z,
∴k=-1,则φ=- .
.
(2)由(1)得:f(x)=sin ,
,
令- +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z,
+2kπ,k∈Z,
可解得 ,k∈Z,
,k∈Z,
因此y=f(x)的单调增区间为 ,k∈Z.
,k∈Z.

练习册系列答案
相关题目
 =3,则
=3,则 的值等于( )
的值等于( ) tan x)cos x的最小正周期为( ).
tan x)cos x的最小正周期为( ). C.π D.
C.π D.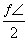
 的最大值为M,最小值为m,则M+m=________.
的最大值为M,最小值为m,则M+m=________.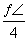 个单位后,再作关于x轴对称变换,得到函数y=1-2sin2x的图象,则f(x)可以是( ).
个单位后,再作关于x轴对称变换,得到函数y=1-2sin2x的图象,则f(x)可以是( ). 时有最大值
时有最大值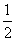 ,当x=
,当x= 时有最小值-
时有最小值- ,则函数解析式f(x)=________.
,则函数解析式f(x)=________. ,cos(α-β)=
,cos(α-β)=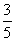 ,则tan αtan β=________.
,则tan αtan β=________.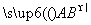 =a+2b,
=a+2b, =-4a-b,
=-4a-b,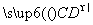 =-5a-3b,则四边形ABCD的形状是( ).
=-5a-3b,则四边形ABCD的形状是( ).