题目内容
6.已知向量$\overrightarrow{a}$=(mcosωx-msinωx,sinωx),$\overrightarrow{b}$=(-cosωx-sinωx,2ncosωx),设函数f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$+$\frac{n}{2}$(x∈R)的图象关于点($\frac{π}{12}$,1)对称,且ω∈(1,2).(I)若m=1,求函数f(x)的最小值;
(Ⅱ)若f(x)≤f($\frac{π}{4}$)对一切实数恒成立,求y=f(x)的单调递增区间.
分析 (I)通过平面向量数量积的运算即倍角公式、辅助角公式化简可知f(x)=$\sqrt{4+{m}^{2}}$sin(2ωx-φ)+1,利用m=1及三角函数的有界性即得结论;
(Ⅱ)通过f(x)≤f($\frac{π}{4}$)对一切实数恒成立可知,当x=$\frac{π}{4}$时g(x)=sin(2ωx-φ)取最大值1,利用当x=$\frac{π}{12}$时g(x)=sin(2ωx-φ)取值为0,可知ω=6(k±$\frac{1}{4}$)(k为整数),进而可知确定函数f(x)的周期,通过求出一个单调区间,利用周期性可得所有的单调递增区间.
解答 解:∵向量$\overrightarrow{a}$=(mcosωx-msinωx,sinωx),$\overrightarrow{b}$=(-cosωx-sinωx,2ncosωx),
∴$\overrightarrow{a}$$•\overrightarrow{b}$=(mcosωx-msinωx)(-cosωx-sinωx)+(sinωx)(2ncosωx)
=-m(cosωx-sinωx)(cosωx+sinωx)+nsin2ωx
=-mcos2ωx+nsin2ωx
=$\sqrt{{m}^{2}+{n}^{2}}$sin(2ωx-φ),
又∵函数f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$+$\frac{n}{2}$(x∈R)的图象关于点($\frac{π}{12}$,1)对称,
∴当x=$\frac{π}{12}$时sin(2ωx-φ)=0,
∴$\frac{n}{2}$=1,即n=2,
∴f(x)=$\sqrt{4+{m}^{2}}$sin(2ωx-φ)+1.
(I)当m=1时,f(x)=$\sqrt{5}$sin(2ωx-φ)+1,
∵-1≤sin(2ωx-φ)≤1,
∴函数f(x)的最小值为1-$\sqrt{5}$;
(Ⅱ)∵f(x)≤f($\frac{π}{4}$)对一切实数恒成立,
∴当x=$\frac{π}{4}$时,g(x)=sin(2ωx-φ)取最大值1,
又∵函数f(x)的图象关于点($\frac{π}{12}$,1)对称,
∴当x=$\frac{π}{12}$时,g(x)=sin(2ωx-φ)取值为0,
∴$\frac{π}{4}$-$\frac{π}{12}$=(k±$\frac{1}{4}$)•$\frac{2π}{2ω}$,即ω=6(k±$\frac{1}{4}$)(k为整数),
又∵ω∈(1,2),
∴ω=$\frac{3}{2}$,即函数f(x)是周期T=$\frac{2π}{2ω}$=$\frac{2π}{3}$的周期函数,
∴y=f(x)的一个单调递增区间为:(-$\frac{π}{12}$,$\frac{π}{4}$),
∴y=f(x)的单调递增区间为:(-$\frac{π}{12}$+$\frac{2kπ}{3}$,$\frac{π}{4}$+$\frac{2kπ}{3}$),k∈Z.
点评 本题以平面向量为载体,考查三角函数的性质,涉及三角函数的倍角公式及辅助角公式等基础知识,考查运算求解能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{15}{2}$ | B. | $\frac{5\sqrt{2}}{3}$ | C. | 5$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
 如图,在实施棚户区改造工程中,某居委会决定对AF地段上的危旧房进行推平改建,拟在EF地段上新建一幢居民安置楼,在EF安置楼正南面的AB地段上建一个活动中心,活动中心的侧面图由两部分构成,下部分ABCD是矩形,上部分是以CD为直径的半圆O,活动中心的规划设计需满足以下要求:①AE=30米;②AB≥AD;③当地“最斜光线”与水平线的夹角α满足tanα=$\frac{3}{4}$,活动中心在当地“最斜光线”照射下落在EF安置楼上的影长GE不超过$\frac{5}{2}$米.
如图,在实施棚户区改造工程中,某居委会决定对AF地段上的危旧房进行推平改建,拟在EF地段上新建一幢居民安置楼,在EF安置楼正南面的AB地段上建一个活动中心,活动中心的侧面图由两部分构成,下部分ABCD是矩形,上部分是以CD为直径的半圆O,活动中心的规划设计需满足以下要求:①AE=30米;②AB≥AD;③当地“最斜光线”与水平线的夹角α满足tanα=$\frac{3}{4}$,活动中心在当地“最斜光线”照射下落在EF安置楼上的影长GE不超过$\frac{5}{2}$米.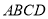 为圆
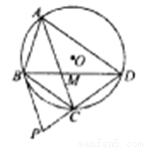
为圆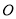 的内接四边形,且
的内接四边形,且 ,其对角线
,其对角线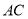 与
与 相交于点
相交于点 ,过点
,过点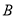 作圆
作圆 的切线交
的切线交 的延长线于点
的延长线于点 .
.
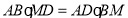 ;
;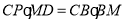 ,求证:
,求证: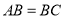 .
.