题目内容

14．已知函数f（x）$\left\{\begin{array}{l}{{a}^{x}lo{g}_{2}x，x＞0}\\{{a}^{x}+lo{g}_{2}（-x），x＜0}\end{array}\right.$（a＞0且a≠1），若f（2）+f（-2）=$\frac{21}{4}$，则a=2或$\frac{1}{2}$．

分析 化简f（2）=a2，f（-2）=$\frac{1}{{a}^{2}}$+1，从而可得a2+$\frac{1}{{a}^{2}}$=$\frac{17}{4}$，从而求得．

解答 解：f（2）=a2，f（-2）=$\frac{1}{{a}^{2}}$+1，
故f（2）+f（-2）=a2+$\frac{1}{{a}^{2}}$+1=$\frac{21}{4}$，
则a2+$\frac{1}{{a}^{2}}$=$\frac{17}{4}$，
故a2=4或a2=$\frac{1}{4}$，
故a=2或a=$\frac{1}{2}$，
故答案为：2或$\frac{1}{2}$．

点评 本题考查了分段函数的应用及分类讨论的思想应用．

练习册系列答案
相关题目
8．在△ABC中，a，b，c分别为角A，B，C的对边，且$\frac{c}{b}$=-3cosA，tanB=$\frac{1}{2}$．
（1）求tanA；
（2）若b=$\sqrt{5}$，求sinC．
6．已知在梯形ABCD中，AB∥CD，AD⊥AB，AB=2，AD=CD=1，将梯形ABCD沿对角线AC折叠成三棱锥D-ABC，当二面角D-AC-B是直二面角时，三棱锥D-ABC的外接球的表面积为4π．
2．在△ABC中，sin2B=2sinA•sinC．
（1）若a=b，求cosB；
（2）若B=90°，且a=$\sqrt{2}$，求△ABC的面积S．
9．已知一元二次方程ax2+bx+c=0的解是-2，3，且a＜0，那么ax2+bx+c＞0的解集是（-2，3）．
19．在平面直角坐标系中，已知动点M到两定点F1（-1，0）和F2（1，0）的距离之和为2$\sqrt{2}$，过点F1作直线与M的轨迹交于A，B两点．
（1）求动点M的轨迹方程；
（2）求△ABF2的周长．
6．已知向量$\overrightarrow{a}$=（mcosωx-msinωx，sinωx），$\overrightarrow{b}$=（-cosωx-sinωx，2ncosωx），设函数f（x）=$\overrightarrow{a}$$•\overrightarrow{b}$+$\frac{n}{2}$（x∈R）的图象关于点（$\frac{π}{12}$，1）对称，且ω∈（1，2）．
（I）若m=1，求函数f（x）的最小值；
（Ⅱ）若f（x）≤f（$\frac{π}{4}$）对一切实数恒成立，求y=f（x）的单调递增区间．
3．己知集合M={x|x2+x+3=0}，则下列结论正确的是（　　）
A．集合M中共有2个元素B．集合M中共有2个相同元素
C．集合M中共有1个元素D．集合M为空集

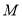已知圆柱的底面半径为2，高为6，圆锥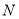的底面直径和母线长相等，若圆柱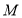和圆锥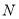的体积相同，则圆锥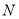的高为 .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网