Question

已知复数|z|=2,求复数1+i+z的模的最大值、最小值.

Answer 1

思路分析:(1)可以由复数的几何意义采用数形结合的方法来解,(2)通过不等式||z₁|-|z₂||≤|z₁+z₂|≤|z₁|+|z₂|,其中第一个等号成立的条件是复数z₁,z₂对应的向量反向共线,第二个等号成立的条件是复数z₁,z₂对应的向量同向共线.

解:法一:由已知,复数z对应的点Z在复平面内以原点为圆心,半径为2的圆上,设ω=1+i+z,∴z=ω-1-i.

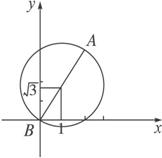
∴|z|=|ω-(1+i)|=2.∴复数ω对应的点在复平面内以(1,)为圆心,半径为2的圆上,此时圆上的点A对应的复数ω_A的模有最大值,圆上的点B对应的复数ω_B的模有最小值.如图,故|1+i+z|_max=4,|1+i+z|_min=0.

法二:利用公式||z₁|-|z₂||≤|z₁+z₂|≤|z₁|+|z₂|.

∵|z|=2,

∴||z|-|1+i||≤|z+1+i|≤|z|+|1+i|,

∴0≤|z+1+i|≤2+2.

∴|1+i+z|_max=4,|1i+z|_min=0.