题目内容
设P是双曲线
-
=1(a>0,b>0)上的点,F1、F2是焦点,双曲线的离心率是
,且∠F1PF2=90°,△F1PF2面积是9,则a+b=( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 4 |
| A、4 | B、5 | C、6 | D、7 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线的定义、勾股定理,△F1PF2面积是9,可得c2-a2=9,结合双曲线的离心率是
=
,求出a,c,可得b,即可求出a+b的值.
| c |
| a |
| 5 |
| 4 |
解答:
解:设|PF1|=m,|PF2|=n,则|m-n|=2a①
由∠F1PF2=90°,可得m2+n2=4c2,②
则①2-②得:-2mn=4a2-4c2,
∴mn=2c2-2a2,
∵△F1PF2面积是9,
∴c2-a2=9,
∵双曲线的离心率是
=
,
∴c=5,a=4,
∴b=3,
∴a+b=7.
故选:D.
由∠F1PF2=90°,可得m2+n2=4c2,②
则①2-②得:-2mn=4a2-4c2,
∴mn=2c2-2a2,
∵△F1PF2面积是9,
∴c2-a2=9,
∵双曲线的离心率是
| c |
| a |
| 5 |
| 4 |
∴c=5,a=4,
∴b=3,
∴a+b=7.
故选:D.
点评:本题主要考查双曲线的基本性质.在涉及到与焦点有关的题目时,一般都用定义求解.

练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边分别是2、3、4,则三角形中最大角的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、-
|
函数y=
的图象如图所示,则( )
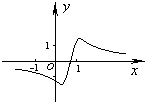
| 2(x+a) |
| (x+a)2+b |

| A、a∈(0,1),b∈(0,1) |
| B、a∈(0,1),b∈(1,+∞) |
| C、a∈(-1,0),b∈(1,+∞) |
| D、a∈(-1,0),b∈(0,1) |
已知实数x,y满足
,则Z=2x-y的最小值是( )
|
| A、3 | B、-3 | C、5 | D、-5 |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,则这两个平面平行;
②若两个平面都垂直于同一条直线,则这两个平面平行;
③若两个平面互相垂直,则在其中一个平面内的直线垂直另外一个平面;
④两个平行直线能确定一个平面,其中正确的命题是( )
①若一个平面内的两条直线与另一个平面都平行,则这两个平面平行;
②若两个平面都垂直于同一条直线,则这两个平面平行;
③若两个平面互相垂直,则在其中一个平面内的直线垂直另外一个平面;
④两个平行直线能确定一个平面,其中正确的命题是( )
| A、①和② | B、②和③ |
| C、③和④ | D、②和④ |
下列函数中,最小正周期为π的是( )
| A、y=|sinx| | ||
| B、y=sinx | ||
C、y=tan
| ||
| D、y=cos4x |
已知函数f(x)=sin(ωx+
)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=sinωx的图象,只要将y=f(x)的图象( )
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
等差数列{an}的公差d<0,且a32=a112,则该数列的前n项和取得最大值时,n=( )
| A、6 | B、7 | C、6或7 | D、7或8 |
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a11,4为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a11,4为