题目内容
已知向量m＝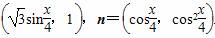
(1)若m·n＝1，求cos
的值；
(2)记f(x)＝m·n，在△ABC中，角A，B，C的对边分别是a，
b，c，且满足(2a－c)cos B＝bcos C，求函数f(A)的取值范围．
(2)因为(2a－c)cos B＝bcos C，
由正弦定理得(2sin A－sin C)cos B＝sin Bcos C，
即2sin Acos B－sin Ccos B＝sin Bcos C，
所以2sin Acos B＝sin(B＋C)，(8分)
又因为A＋B＋C＝π，
所以sin(B＋
C)＝sin A，且sin A≠0，
练习册系列答案
名校课堂系列答案
相关题目
，求
的值。
，且函数
的最小正周期为
。
中，角A,B,C所对的边分别为a,b,c，若
的值。
2，CD＝4，E为边DC的中点，如图1.将△ADE沿AE折起到△AEP位置，连PB、PC，点Q是棱AE的中点，点M在棱PC上，如图2.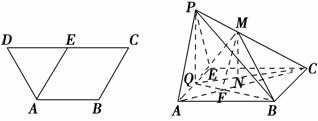
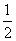，若存在实数p，q，对任意n∈N*都有p≤T1＋T2＋T3＋…＋Tn＜q成立，试求q－p的最小值．
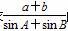的值；
的展开式中
的系数为 ．