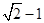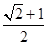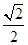题目内容
椭圆 上的一点
上的一点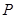 ,它到椭圆的一个焦点
,它到椭圆的一个焦点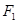 的距离是7,则它到另一个焦点
的距离是7,则它到另一个焦点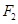 的距离是( )
的距离是( )
A.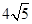 | B.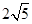 | C.12 | D.5 |
D
解析试题分析:先根据条件椭圆方程 求出a=6;再根据椭圆定义得到关于所求距离d的等式即可得到结论。设所求距离为d,由题得:a=6.根据椭圆的定义得:2a=7+d⇒d=2a-7=54.故可知d=5,那么
求出a=6;再根据椭圆定义得到关于所求距离d的等式即可得到结论。设所求距离为d,由题得:a=6.根据椭圆的定义得:2a=7+d⇒d=2a-7=54.故可知d=5,那么
故选D.
考点:本题主要考查椭圆的定义的运用。利用椭圆的定义和方程得到a,b,c的值,进而求解得到。
点评:解决涉及到圆锥曲线上的点与焦点之间的关系的问题中,圆锥曲线的定义往往是解题的突破口。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
双曲线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C. | D. |
双曲线两条渐近线互相垂直,那么它的离心率为 ( )
| A.2 | B.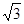 | C.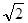 | D.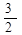 |
设P是双曲线 与圆
与圆 在第一象限的交点,
在第一象限的交点, 分别是双曲线的左右焦点,且
分别是双曲线的左右焦点,且 则双曲线的离心率为( )
则双曲线的离心率为( )
A. | B. | C.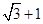 | D.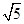 |
设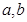 是方程x
是方程x =0的两个实根,那么过点
=0的两个实根,那么过点 和
和  (
( )的直线与椭圆
)的直线与椭圆 的位置关系是
的位置关系是
| A.相交 | B.相切 | C.相交或相切 | D.相离 |
已知AB是过椭圆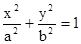 (a>b>0)的左焦点F1的弦,则⊿ABF2的周长是( )
(a>b>0)的左焦点F1的弦,则⊿ABF2的周长是( )
| A.a | B.2a | C.3ª | D.4a |
 ,
, 、
、 分别是它的左、右焦点,若过
分别是它的左、右焦点,若过 是
是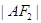 与
与 的等差中项,则
的等差中项,则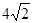

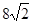
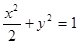 的右焦点作倾斜角为
的右焦点作倾斜角为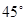 的直线
的直线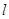 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则 ( )
( )

 ,
, ,过
,过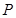 ,若△
,若△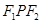 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )