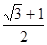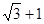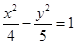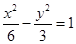题目内容
设P是双曲线 与圆
与圆 在第一象限的交点,
在第一象限的交点, 分别是双曲线的左右焦点,且
分别是双曲线的左右焦点,且 则双曲线的离心率为( )
则双曲线的离心率为( )
A. | B. | C.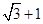 | D.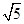 |
D
解析试题分析:P点在双曲线右支上,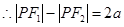 又
又
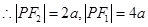
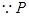 点在圆
点在圆 上
上 即
即

考点:双曲线定义离心率
点评:求离心率需找a,c的齐次方程

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线 与曲线
与曲线 相切于点
相切于点 ,则
,则 的值为 ( )
的值为 ( )
| A.-3 | B.9 |
| C.-15 | D.-7 |
若椭圆的短轴为 ,它的一个焦点为F1,则满足
,它的一个焦点为F1,则满足 为等边三角形的椭圆的离心率是( )
为等边三角形的椭圆的离心率是( )
A. | B. | C. | D. |
椭圆 上的一点
上的一点 ,它到椭圆的一个焦点
,它到椭圆的一个焦点 的距离是7,则它到另一个焦点
的距离是7,则它到另一个焦点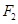 的距离是( )
的距离是( )
A.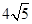 | B.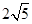 | C.12 | D.5 |
已知曲线C:  与抛物线
与抛物线 的一个交点为M,
的一个交点为M, 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为
A. | B.- | C. | D.- |
抛物线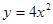 的焦点坐标是( )
的焦点坐标是( )
A. | B.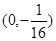 | C. | D.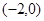 |
若焦点在 轴上的椭圆
轴上的椭圆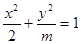 的离心率为
的离心率为 ,则
,则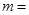 ( )
( )
A.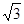 | B.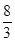 | C.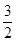 | D.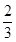 |
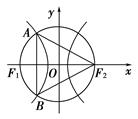
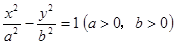 的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则离心率为( )
的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则离心率为( )