题目内容
已知AB是过椭圆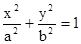 (a>b>0)的左焦点F1的弦,则⊿ABF2的周长是( )
(a>b>0)的左焦点F1的弦,则⊿ABF2的周长是( )
| A.a | B.2a | C.3ª | D.4a |
D
解析试题分析:根据椭圆的定义可知:|F1A|+|AF2|=2a=,|F1B|+|BF2|=2a,
如图所示:
∴△ABF2的周长为|F1A|+|AF2|+|F1B|+|BF2|=4a,
故答案为D
考点:本试题主要考查了椭圆的定义,属于基础题,当曲线上的点与曲线的焦点连线时首先考虑定义.
点评:解决该试题的关键是由椭圆的定义可知:|F1A|+|AF2|=2a=,|F1B|+|BF2|=2a,再结合椭圆的图象将其转化为三角形的周长.

练习册系列答案
相关题目
椭圆 上的一点
上的一点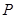 ,它到椭圆的一个焦点
,它到椭圆的一个焦点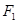 的距离是7,则它到另一个焦点
的距离是7,则它到另一个焦点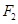 的距离是( )
的距离是( )
A.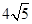 | B.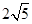 | C.12 | D.5 |
抛物线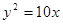 的焦点到准线的距离是
的焦点到准线的距离是
A.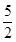 | B.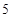 | C.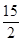 | D.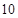 |
抛物线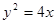 上一点
上一点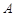 的横坐标为4,则点
的横坐标为4,则点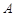 与抛物线焦点的距离为
与抛物线焦点的距离为
| A.2 | B.3 | C.4 | D.5 |
抛物线  的准线方程是( ).
的准线方程是( ).
A.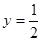 | B. | C.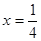 | D.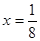 |
若焦点在 轴上的椭圆
轴上的椭圆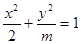 的离心率为
的离心率为 ,则
,则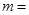 ( )
( )
A.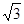 | B.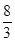 | C.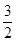 | D.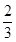 |
过双曲线 的右焦点
的右焦点 作圆
作圆 的切线
的切线 (切点为
(切点为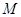 ),交
),交 轴于点
轴于点 . 若
. 若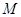 为线段
为线段 的中点,则双曲线的离心率是
的中点,则双曲线的离心率是
| A.2 | B. | C. | D. |
已知经过椭圆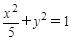 的焦点且与其对称轴成
的焦点且与其对称轴成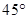 的直线与椭圆交于
的直线与椭圆交于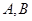 两点,
两点,
则|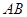 |=( ).
|=( ).
A.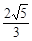 | B.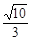 | C.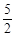 | D.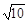 |
设 是椭圆
是椭圆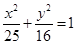 上的点.若
上的点.若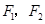 是椭圆的两个焦点,则
是椭圆的两个焦点,则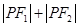 等于( )
等于( )
| A.4 | B.5 | C.8 | D.10 |