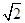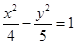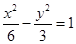题目内容
设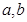 是方程x
是方程x =0的两个实根,那么过点
=0的两个实根,那么过点 和
和  (
( )的直线与椭圆
)的直线与椭圆 的位置关系是
的位置关系是
| A.相交 | B.相切 | C.相交或相切 | D.相离 |
A
解析试题分析:由于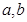 是方程x
是方程x =0的两个实根,则判别式大于等于零,可知tan2
=0的两个实根,则判别式大于等于零,可知tan2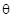 +8cos
+8cos 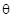
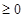 ,a+b=tan
,a+b=tan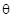 ,ab=-2cos
,ab=-2cos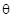 ,那么直线AB的斜率为k=b+a,那么即为k=tan
,那么直线AB的斜率为k=b+a,那么即为k=tan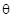 ,而曲线
,而曲线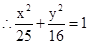 ,直线AB:y-
,直线AB:y- ,联立方程组可知结论为相交或相切,选A.
,联立方程组可知结论为相交或相切,选A.
考点:本题主要考查了直线与椭圆的位置关系的运用。
点评:解决该试题的关键是利用方程有两个实根,得到方程的两个根,然后利用联立方程组的思想得到直线与椭圆的位置关系。

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
椭圆 上的一点
上的一点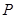 ,它到椭圆的一个焦点
,它到椭圆的一个焦点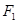 的距离是7,则它到另一个焦点
的距离是7,则它到另一个焦点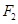 的距离是( )
的距离是( )
A.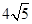 | B.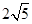 | C.12 | D.5 |
已知曲线C: 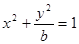 与抛物线
与抛物线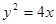 的一个交点为M,
的一个交点为M,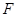 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为
A.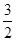 | B.-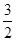 | C. | D.- |
抛物线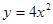 的焦点坐标是( )
的焦点坐标是( )
A. | B.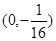 | C. | D.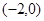 |
抛物线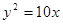 的焦点到准线的距离是
的焦点到准线的距离是
A.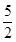 | B.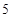 | C.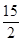 | D.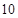 |
抛物线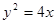 上一点
上一点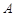 的横坐标为4,则点
的横坐标为4,则点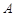 与抛物线焦点的距离为
与抛物线焦点的距离为
| A.2 | B.3 | C.4 | D.5 |
已知经过椭圆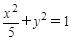 的焦点且与其对称轴成
的焦点且与其对称轴成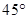 的直线与椭圆交于
的直线与椭圆交于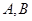 两点,
两点,
则|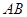 |=( ).
|=( ).
A.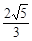 | B.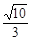 | C.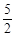 | D.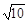 |