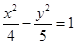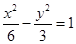题目内容
设椭圆的两个焦点分别为 ,
, ,过
,过 作椭圆长轴的垂线与椭圆相交,其中的一个交点为
作椭圆长轴的垂线与椭圆相交,其中的一个交点为 ,若△
,若△ 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )
A.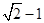 | B.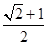 | C. | D.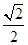 |
A
解析试题分析: 设椭圆的方程为 ,那么设点P(c,h),则
,那么设点P(c,h),则 ,可知
,可知 ,由题意得∠F1PF2=90°,∠PF1F2=45°,Rt△PF1F2 中,tan45°="1,"
,由题意得∠F1PF2=90°,∠PF1F2=45°,Rt△PF1F2 中,tan45°="1,"  ,∴a2-c2=2ac,两边同时除以解得a2,得到e=
,∴a2-c2=2ac,两边同时除以解得a2,得到e= 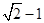 ,故选A.
,故选A.
考点:本题主要考查了椭圆的简单性质,直角三角形中的边角关系的应用.考查计算能力.
点评:解决该试题的关键是设椭圆的方程和点P的坐标,把点P的坐标代入椭圆的方程,求出点P的纵坐标的绝对值,Rt△PF1F2 中,利用边角关系,建立a、c 之间的关系,从而求出椭圆的离心率.

练习册系列答案
相关题目
已知椭圆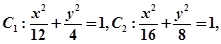 则 ( )
则 ( )
A.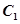 与 与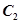 顶点相同. 顶点相同. | B.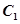 与 与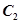 长轴长相同. 长轴长相同. |
C.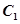 与 与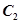 短轴长相同. 短轴长相同. | D.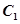 与 与 焦距相等. 焦距相等. |
若方程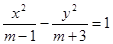 表示双曲线,则实数
表示双曲线,则实数 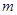 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
C.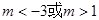 | D. |
椭圆 上的一点
上的一点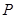 ,它到椭圆的一个焦点
,它到椭圆的一个焦点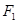 的距离是7,则它到另一个焦点
的距离是7,则它到另一个焦点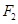 的距离是( )
的距离是( )
A.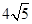 | B.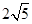 | C.12 | D.5 |
双曲线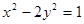 的右焦点的坐标为( )
的右焦点的坐标为( )
A.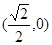 | B.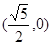 | C. | D.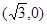 |
已知曲线C: 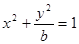 与抛物线
与抛物线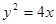 的一个交点为M,
的一个交点为M,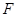 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为
A.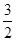 | B.-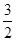 | C. | D.- |
抛物线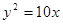 的焦点到准线的距离是
的焦点到准线的距离是
A.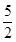 | B.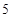 | C.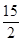 | D.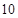 |
过双曲线 的右焦点
的右焦点 作圆
作圆 的切线
的切线 (切点为
(切点为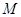 ),交
),交 轴于点
轴于点 . 若
. 若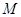 为线段
为线段 的中点,则双曲线的离心率是
的中点,则双曲线的离心率是
| A.2 | B. | C. | D. |