题目内容
已知抛物线C:y2=4x,焦点为F,准线与x轴交于点A,过A且斜率为k的直线l与抛物线C交于P、Q两点,求满足
=
+
的点R的轨迹方程.
| FR |
| FP |
| FQ |
考点:轨迹方程
专题:向量与圆锥曲线
分析:由抛物线方程求出准线方程及焦点坐标,进一步求出A的坐标和直线l的方程,联立直线方程与圆锥抛物线方程,利用根与系数的关系得到P,Q两点横纵坐标的和,结合
=
+
由向量的坐标加法运算得到R的坐标与P,Q坐标的关系,得到R的参数方程,消去参数k后得答案.
| FR |
| FP |
| FQ |
解答:
解:由y2=4x,得其准线方程为x=-1,即A(-1,0),焦点F(1,0),
则直线l的方程为y-0=k(x+1),
联立
,消去y得:k2x2+(2k2-4)x+k2=0.
设P(x1,y1),Q(x2,y2),R(x,y),
则x1+x2=
,x1x2=1,x1+x2-1=
-1=
,
y1+y2=k(x1+x2)+2k=
+2k=
.
=(x-1,y),
=(x1-1,y1),
=(x2-1,y2),
由
=
+
,得
,即
.
∴
,消去k得:y2=4x+12.
∴满足
=
+
的点R的轨迹方程为y2=4x+12.
则直线l的方程为y-0=k(x+1),
联立
|
设P(x1,y1),Q(x2,y2),R(x,y),
则x1+x2=
| 4-2k2 |
| k2 |
| 4-2k2 |
| k2 |
| 4-3k2 |
| k2 |
y1+y2=k(x1+x2)+2k=
| 4-2k2 |
| k |
| 4 |
| k |
| FR |
| FP |
| FQ |
由
| FR |
| FP |
| FQ |
|
|
∴
|
∴满足
| FR |
| FP |
| FQ |
点评:本题考查了轨迹方程的求法,考查了向量的坐标运算,训练了向量在解圆锥曲线题中的应用,是中档题.

练习册系列答案
相关题目
设全集为I,则表示右图中阴影部分的集合是( )


| A、A∪B |
| B、A∩B |
| C、(∁IA)∪(∁IB) |
| D、(∁IA)∩(∁IB) |
已知数列{an}是等差数列,a3=-2,前6项的和S6=-3,那么数列{n+an}的前4项的和是( )
| A、-4 | B、-1 | C、5 | D、6 |
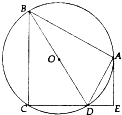 如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.
如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA. 求曲线y=sinx,y=cosx与直线x=0,x=
求曲线y=sinx,y=cosx与直线x=0,x=