题目内容
若正三棱锥的棱长为6cm,求它的内切球的表面积为 .
考点:球的体积和表面积
专题:计算题,空间位置关系与距离,球
分析:求出正三棱锥的高,求出正三棱锥的全面积和体积,设内切球的半径为r,以球心O为顶点,以棱锥的四个面为底面把正三棱锥分割为四个小棱锥,运用等积法可得球的半径,即可求出球的表面积.
解答:
解:由题意,底面外接圆的半径为
×
×6=2
,
∴正三棱锥的高为
=2
,
∵正三棱锥的所有棱长都等于6,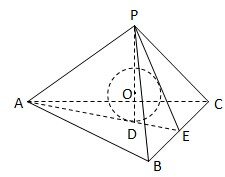
则S全=4×
×62=36
.VP-ABC=
×
×36×2
=18
,
设内切球的半径为r,以球心O为顶点,
以棱锥的四个面为底面把正三棱锥分割为四个小棱锥,
则V1+V2+V3+V4=
rS全=VP-ABC,
∴r=
=
=
,
∴S球=4πr2=4π×
=6π.
故答案为:6π.
| 2 |
| 3 |
| ||
| 2 |
| 3 |
∴正三棱锥的高为
62-(2
|
| 6 |
∵正三棱锥的所有棱长都等于6,

则S全=4×
| ||
| 4 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 6 |
| 2 |
设内切球的半径为r,以球心O为顶点,
以棱锥的四个面为底面把正三棱锥分割为四个小棱锥,
则V1+V2+V3+V4=
| 1 |
| 3 |
∴r=
| 3VP-ABC |
| S全 |
3×18
| ||
36
|
| ||
| 2 |
∴S球=4πr2=4π×
| 6 |
| 4 |
故答案为:6π.
点评:本题考查正三棱锥与内切球的关系,主要考查球的表面积公式的计算,确定球的半径是关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了解该单位职工的心理状况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为( )
| A、7 | B、15 | C、35 | D、25 |
若sin(
+α)=
,则cos(
-α)=( )
| π |
| 6 |
| 3 |
| 5 |
| π |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
一个棱长为1的正方形的顶点都在球面上,则这个球面的表面积是( )
| A、π | B、3π | C、4π | D、12π |
已知双曲线x2-
=1(b>0)的离心率
,则b等于( )
| y2 |
| b2 |
| 10 |
| A、2 | B、3 | C、4 | D、5 |
设向量
=(1,2),
=(-2,1),则下列结论中不正确的是( )
| a |
| b |
A、|
| ||||||||
B、(
| ||||||||
C、|
| ||||||||
D、
|
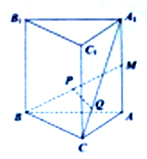 在直三棱柱ABC-A1B1C1中,若BC⊥AC,∠A=
在直三棱柱ABC-A1B1C1中,若BC⊥AC,∠A=