题目内容
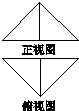
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
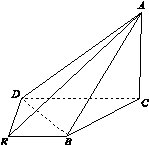
图15
解:(1)证明:在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC= ,
,
由AC= ,AB=2,
,AB=2,
得AB2=AC2+BC2,即AC⊥BC.
又平面ABC⊥平面BCDE,从而AC⊥平面BCDE,
所以AC⊥DE.又DE⊥DC,从而DE⊥平面ACD.
(2)方法一:
过B作BF⊥AD,与AD交于点F,过点F作FG∥DE,与AE交于点G,连接BG.由(1)知DE⊥AD,则FG⊥AD.所以∠BFG是二面角B AD E的平面角.
在直角梯形BCDE中,由CD2=BC2+BD2,
得BD⊥BC.
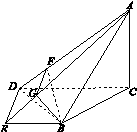
又平面ABC⊥平面BCDE,得BD⊥平面ABC,从而BD⊥AB.由AC⊥平面BCDE,得AC⊥CD.
在Rt△ACD中,由DC=2,AC= ,得AD=
,得AD=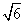 .
.
在Rt△AED中,由ED=1,AD=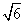 ,得AE=
,得AE=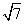 .
.
在Rt△ABD中,由BD= ,AB=2,AD=
,AB=2,AD=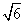 ,得BF=
,得BF=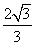 ,AF=
,AF=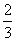 AD.从而GF=
AD.从而GF=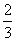 ED=
ED=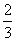 .
.
在△ABE,△ABG中,利用余弦定理分别可得cos∠BAE=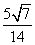 ,BG=
,BG=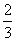 .
.
在△BFG中,cos∠BFG=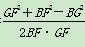 =
= .
.
所以,∠BFG= ,即二面角B AD E的大小是
,即二面角B AD E的大小是 .
.
方法二:
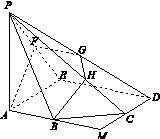
以D为原点,分别以射线DE,DC为x,y轴的正半轴,建立空间直角坐标系D xyz,如图所示.

由题意知各点坐标如下:
D(0,0,0),E(1,0,0),C(0,2,0),
A(0,2, ),B(1,1,0).
),B(1,1,0).
设平面ADE的法向量为m=(x1,y1,z1),
平面ABD的法向量为n=(x2,y2,z2).
可算得AD=(0,-2,- ),AE=(1,-2,-
),AE=(1,-2,- ),
),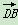 =(1,1,0).
=(1,1,0).


在一块耕地上种植一种作物,每季种植成本为1 000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
| 作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| 作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.4 | 0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2 000元的概率.
 C.1 D.
C.1 D.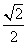
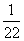 B.
B.
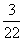 D.
D.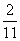
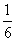 B.
B.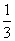
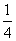 D.
D.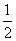
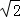 ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.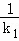 +
+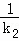 +
+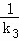 为定值.
为定值.